 Presh Talwalkar presented an interesting puzzle that originated in the Ladies’ Diary of 1739-40, was recast by Henry Dudeney in 1917, and further modified using American money.
Presh Talwalkar presented an interesting puzzle that originated in the Ladies’ Diary of 1739-40, was recast by Henry Dudeney in 1917, and further modified using American money.
“Each of three Dutchmen, named Hendrick, Elas, and Cornelius has a wife. The three wives have names Gurtrün, Katrün, and Anna (but not necessarily matching the husband’s names in that order). All six go to the market to buy hogs.
Each person buys as many hogs as he or she pays dollars for one. (1 hog costs $1, 2 hogs are $2 each, 3 hogs cost $3 each, etc.) In the end, each husband has spent $63 more than his wife. Hendrick buys 23 more hogs than Katrün, and Elas 11 more than Gurtrün. Now, what is the name of each man’s wife?”
See the Three Dutchmen Puzzle for solutions.
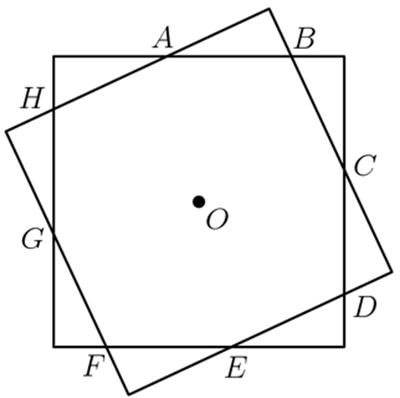 This is a fairly straight-forward problem from the 1999 AIME problems.
This is a fairly straight-forward problem from the 1999 AIME problems.
 Presh Talwalkar presented an interesting puzzle that originated in the Ladies’ Diary of 1739-40, was recast by Henry Dudeney in 1917, and further modified using American money.
Presh Talwalkar presented an interesting puzzle that originated in the Ladies’ Diary of 1739-40, was recast by Henry Dudeney in 1917, and further modified using American money. This is a rather mind-boggling problem from the 1947 Eureka magazine.
This is a rather mind-boggling problem from the 1947 Eureka magazine. This is a nice little puzzle from the 2024 Math Calendar.
This is a nice little puzzle from the 2024 Math Calendar.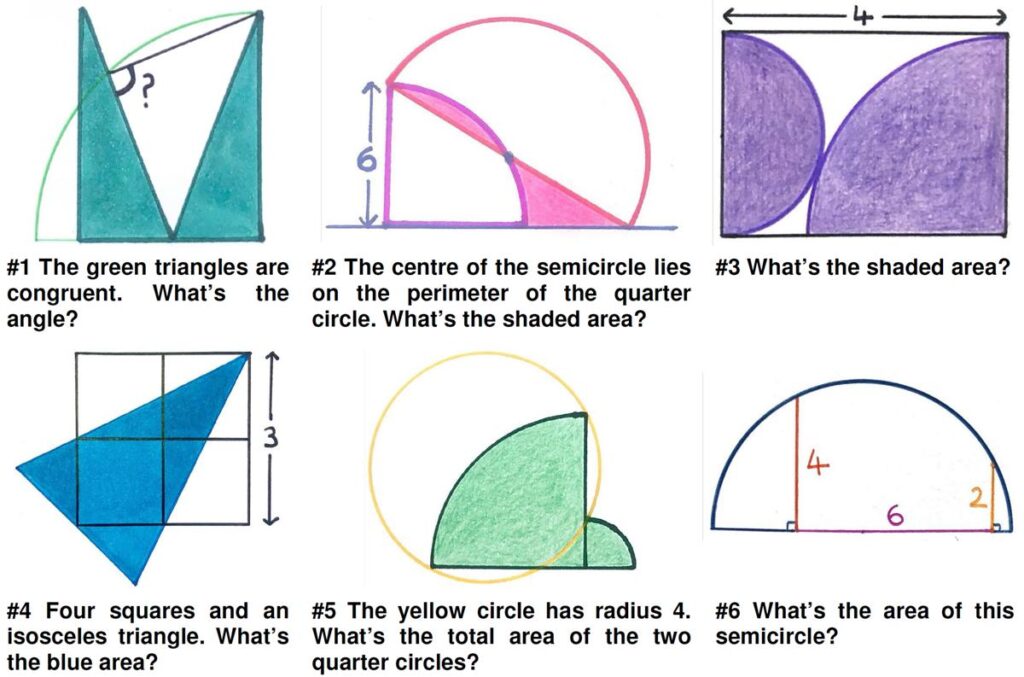
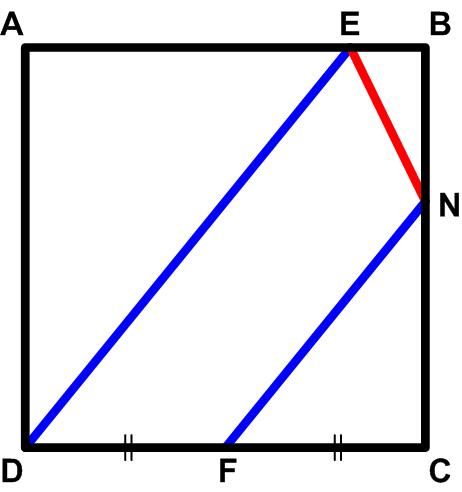 This is an interesting problem from the collection Five Hundred Mathematical Challenges.
This is an interesting problem from the collection Five Hundred Mathematical Challenges. This is a challenging problem from the c.100AD Chinese mathematical work, Jiǔ zhāng suàn shù (The Nine Chapters on the Mathematical Art) found at the MAA Convergence website.
This is a challenging problem from the c.100AD Chinese mathematical work, Jiǔ zhāng suàn shù (The Nine Chapters on the Mathematical Art) found at the MAA Convergence website. This is an interesting problem from 180 BC China.
This is an interesting problem from 180 BC China.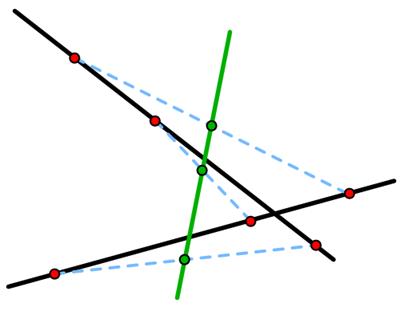 I came across this remarkable
I came across this remarkable 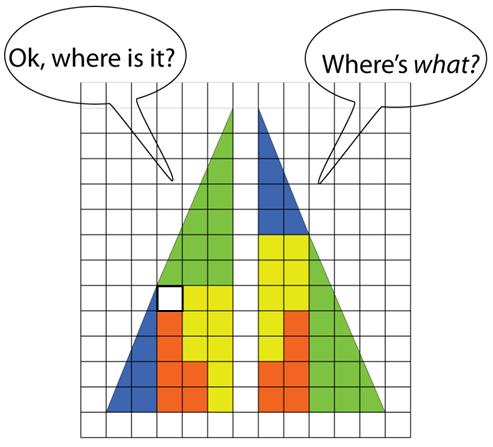 Coming across this
Coming across this