 Here is another problem (slightly edited) from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos).
Here is another problem (slightly edited) from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos).
“Holmes and I were walking along a sleepy lane in Hookland, making our way back to the inn at which we had secured lodgings after scouting out the estates of the supposed major, C. L. Nolan. Up ahead, a team of horses were slowly pulling a chained tree trunk along the lane. Fortunately it had been trimmed of its branches, but it was still an imposing sight.
When we’d overtaken the thing, Holmes surprised me by turning sharply on his heel and walking back along the trunk. I stopped where I was to watch him. He continued at a steady pace until he’d passed the last of it, then reversed himself once more, and walked back to me.
‘Come along, old chap,’ he said as he walked past. Shaking my head, I duly followed.
‘It took me 140 paces to walk from the back of the tree to the front, and just twenty to walk from the front to the back,’ he declared.
‘Well of course,’ I said. ‘The tree was moving, after all.’
‘Precisely,’ he said. ‘My pace is one yard in length, so how long is that tree-trunk?’
Can you find the answer?”
Answer.
See the Tree Trunk Puzzle for solutions.
Post Views: 924


 In my search for problems I decided to purchase Dan Griller’s GCSE problem book mentioned in the
In my search for problems I decided to purchase Dan Griller’s GCSE problem book mentioned in the  Here is a nice logic puzzle from 2014 Futility Closet.
Here is a nice logic puzzle from 2014 Futility Closet. For a change of pace, here is an early
For a change of pace, here is an early 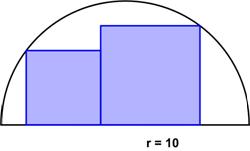 Yet another interesting problem from
Yet another interesting problem from  Here is a collection of puzzles from the great logic puzzle master Raymond Smullyan in a “Brain Bogglers” column for the 1996 Discover magazine.
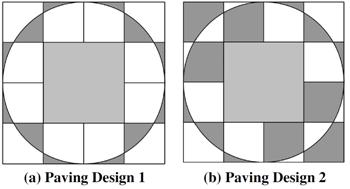
Here is a collection of puzzles from the great logic puzzle master Raymond Smullyan in a “Brain Bogglers” column for the 1996 Discover magazine.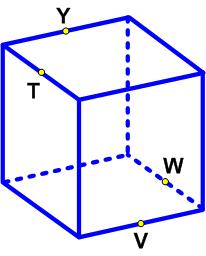 This is a problem from the UKMT Senior Challenge for 2019. (It has been slightly edited to reflect the colors I added to the diagram.)
This is a problem from the UKMT Senior Challenge for 2019. (It has been slightly edited to reflect the colors I added to the diagram.) The following problem comes from a 1961 exam set collected by Ed Barbeau of the University of Toronto. The discontinued exams (by 2003) were for 5th year Ontario high school students seeking entrance and scholarships for the second year at a university.
The following problem comes from a 1961 exam set collected by Ed Barbeau of the University of Toronto. The discontinued exams (by 2003) were for 5th year Ontario high school students seeking entrance and scholarships for the second year at a university. This is a nice Brainteaser from the Quantum math magazine.
This is a nice Brainteaser from the Quantum math magazine. Here is another problem (slightly edited) from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos).
Here is another problem (slightly edited) from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos).