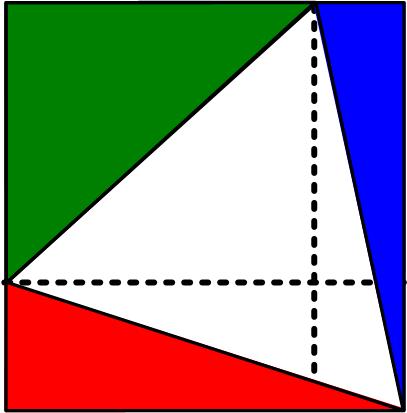
 This simple-appearing problem is from the 17 August 2020 MathsMonday offering by MEI, an independent curriculum development body for mathematics education in the UK.
This simple-appearing problem is from the 17 August 2020 MathsMonday offering by MEI, an independent curriculum development body for mathematics education in the UK.
“The diagram shows an equilateral triangle in a rectangle. The two shapes share a corner and the other corners of the triangle lie on the edges of the rectangle. Prove that the area of the green triangle is equal to the sum of the areas of the blue and red triangles. What is the most elegant proof of this fact?”
Since the MEI twitter page seemed to be aimed at the high school level and the parting challenge seemed to indicate that there was one of those simple, revealing solutions to the problem, I spent several days trying to find one. I went down a number of rabbit holes and kept arriving at circular reasoning results that assumed what I wanted to prove. Visio revealed a number of fascinating relationships, but they all assumed the result and did not provide a proof. I finally found an approach that I thought was at least semi-elegant.
See the Diabolical Triangle Puzzle
(Update 1/30/2021) New MEI Solution

 Here is a fairly straight-forward problem from 500 Mathematical Challenges.
Here is a fairly straight-forward problem from 500 Mathematical Challenges.
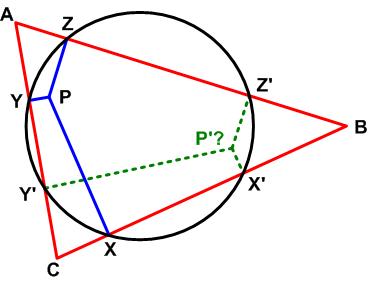 This is an interesting problem from the 1977 Canadian Math Society’s magazine, Crux Mathematicorum.
This is an interesting problem from the 1977 Canadian Math Society’s magazine, Crux Mathematicorum.
 And so another year has passed—a pretty horrible one at that. Hopefully things mathematical have provided a distraction and entertainment.
And so another year has passed—a pretty horrible one at that. Hopefully things mathematical have provided a distraction and entertainment.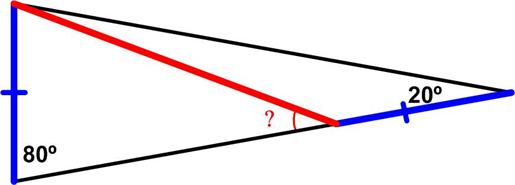 Here is yet another problem from
Here is yet another problem from  Here is another delightful problem from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos).
Here is another delightful problem from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos). This is a nifty little problem from the Quantum math magazine.
This is a nifty little problem from the Quantum math magazine.