 This is a fun logic puzzle from one of Ian Stewart’s many math collections. I discovered that the problem actually is basically one of Lewis Carroll’s examples from an 1896 book:
This is a fun logic puzzle from one of Ian Stewart’s many math collections. I discovered that the problem actually is basically one of Lewis Carroll’s examples from an 1896 book:
- The only animals in this house are cats.
- Every animal that loves to gaze at the moon is suitable for a pet.
- When I detest an animal, I avoid it.
- No animals are meat-eaters, unless they prowl by night.
- No cat fails to kill mice.
- No Animals ever take to me, except those in this house.
- Kangaroos are not suitable for pets.
- Only meat-eaters kill mice.
- I detest animals that do not take to me.
- Animals that prowl at night love to gaze at the moon.
If all these statements are correct, do I avoid kangaroos, or not?
See Do I Avoid Kangaroos? for solutions.

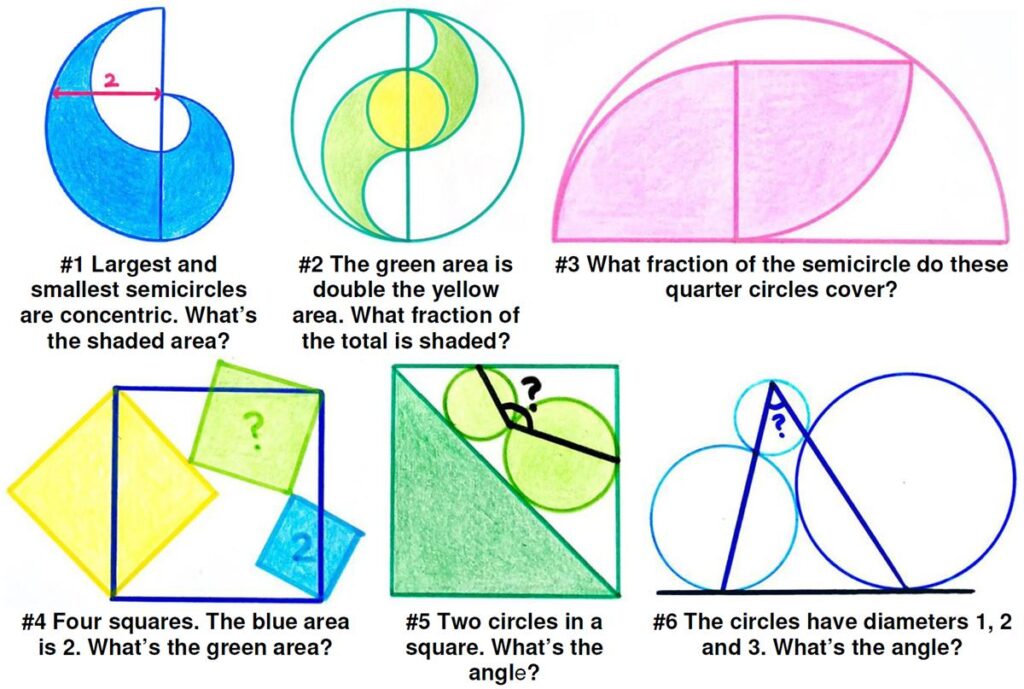
 Here is a simple Futility Closet problem from 2014.
Here is a simple Futility Closet problem from 2014.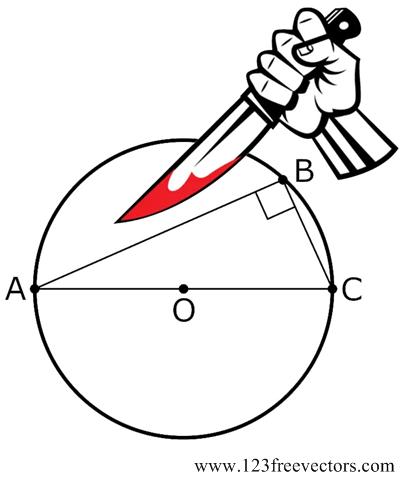 One of my favorite bloggers, Kevin Drum, decided to relieve the tedium of our current political anarchy by whacking the hornets’ nest of the high school mathematics curriculum, in particular the subject of plane geometry. You can tell from the tag list on my blog that I hold plane geometry in high regard and can’t let this gibe pass without some rebuttal, futile as it may be. Actually, I am not going to weigh in on the general issue of the current math curriculum that much, but rather make a few observations from my own experience over the years as it relates to
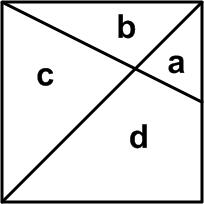
One of my favorite bloggers, Kevin Drum, decided to relieve the tedium of our current political anarchy by whacking the hornets’ nest of the high school mathematics curriculum, in particular the subject of plane geometry. You can tell from the tag list on my blog that I hold plane geometry in high regard and can’t let this gibe pass without some rebuttal, futile as it may be. Actually, I am not going to weigh in on the general issue of the current math curriculum that much, but rather make a few observations from my own experience over the years as it relates to  Here is a problem from Five Hundred Mathematical Challenges that I indeed found quite challenging.
Here is a problem from Five Hundred Mathematical Challenges that I indeed found quite challenging.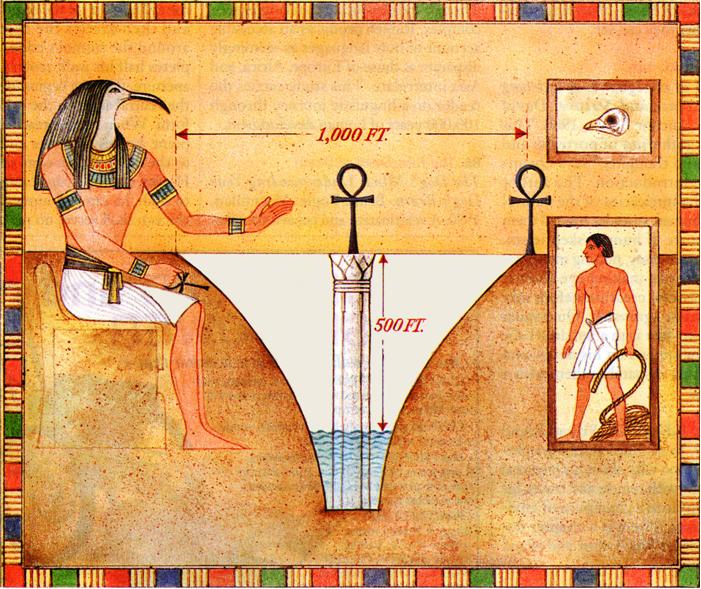 This is a nice puzzle from Clifford Pickover in the 1996 Discover magazine’s Brain Bogglers.
This is a nice puzzle from Clifford Pickover in the 1996 Discover magazine’s Brain Bogglers.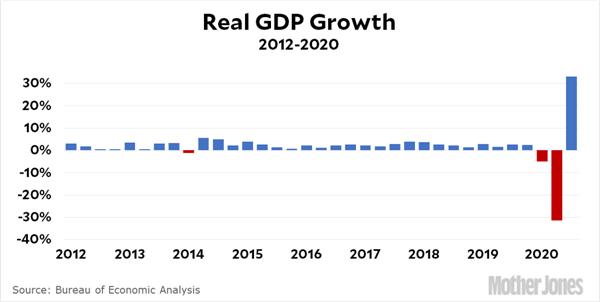 Twitter comments to the recently released GDP growth numbers for the Third Quarter reminded me of an old trap regarding percentages. The financial and technical articles were accurate, but the comments by Twitter users often reflected the pitfall.
Twitter comments to the recently released GDP growth numbers for the Third Quarter reminded me of an old trap regarding percentages. The financial and technical articles were accurate, but the comments by Twitter users often reflected the pitfall. Here is another problem from the 2020 Math Calendar.
Here is another problem from the 2020 Math Calendar.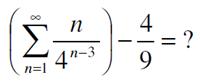
 Again we have a puzzle from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos). This one is quite a bit more challenging, at least for me.
Again we have a puzzle from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos). This one is quite a bit more challenging, at least for me. This is another delightful Brainteaser from the Quantum math magazine.
This is another delightful Brainteaser from the Quantum math magazine.