 This is another challenging puzzle from Presh Talwalkar that seems difficult to know where to start.
This is another challenging puzzle from Presh Talwalkar that seems difficult to know where to start.
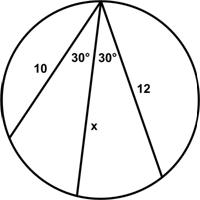
“Given the figure shown at left, what is the value of x?”
See the Chord Progression Puzzle for solutions.

 This is another challenging puzzle from Presh Talwalkar that seems difficult to know where to start.
This is another challenging puzzle from Presh Talwalkar that seems difficult to know where to start.
“Given the figure shown at left, what is the value of x?”
See the Chord Progression Puzzle for solutions.
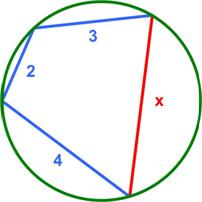
Here is another Brain Bogglers problem from 1987 by Michael Stueben.
“A quadrilateral with sides three, two, and four units in length is inscribed in a circle of diameter five. What’s the length of the fourth side of the quadrilateral?”
Like a number of other Brain Bogglers this problem also uses an insight that makes the solution easy.
See the Quad in Circle Problem for a solution.
 Here is another Brainteaser from the Quantum magazine.
Here is another Brainteaser from the Quantum magazine.
“Prove that the area of the red portion of the star is exactly half the area of the whole star. (N. Avilov)”
This is a relatively simple problem, but I wanted to include it because of its cartoon. Its implied gentle post-Soviet humor reminded me of that strange decade in US-Russian affairs between the end of the Cold War and the rise of Putin in the 21st century. The strangeness was brought home when we had our annual security checks of our classified document storage. Being mostly anti-submarine warfare (ASW) material the main concern was that it would not fall into the hands of the Soviets. But with the “demise” of the Soviet Union in 1989 no one cared any more about the classification. After decades of painfully securing these documents we could not suddenly turn them loose and throw them into the public trash. So we kept them secure anyway. You can imagine how we old cold-warriors feel about the current regime.
That is not to say that I didn’t welcome the thaw. Russian literature, both classical and even “Soviet realism”, as well as Russian cinema, is some of the world’s best. And Russian mathematicians have always been superior, and especially adept at communicating with novices. The collaboration of the American mathematicians and Kvant contributors in Quantum produced excellent results during the thaw. It is unfortunate that it could not survive the rise of Putin and his oligarchs.
See the Red Star
 In looking through some old files I came across a math magazine I had bought in 1998. It was called Quantum and was published by the National Science Teachers Association in collaboration with the Russian magazine Kvant during the period 1990 to 2001 (coinciding with the Russian thaw, which in the following age of Putin seems eons ago). Fortunately, they are all online now. Besides some fascinating math articles the magazine contains a column of “Brainteasers.” Here is one of them:
In looking through some old files I came across a math magazine I had bought in 1998. It was called Quantum and was published by the National Science Teachers Association in collaboration with the Russian magazine Kvant during the period 1990 to 2001 (coinciding with the Russian thaw, which in the following age of Putin seems eons ago). Fortunately, they are all online now. Besides some fascinating math articles the magazine contains a column of “Brainteasers.” Here is one of them:
“Alice used to walk to school every morning, and it took 20 minutes for her from door to door. Once on her way she remembered she was going to show the latest issue of Quantum to her classmates but had forgotten it at home. She knew that if she continued walking to school at the same speed, she’d be there 8 minutes before the bell, and if she went back home for the magazine she’d arrive at school 10 minutes late. What fraction of the way to school had she walked at that moment in time? (S. Dvorianinov)”
This is fairly straight-forward, but other problems in the magazine are a bit more challenging.
See Calculating on the Way for solutions.
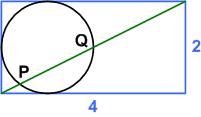 Here is another UKMT Senior Challenge problem from 2017, which has a straight-forward solution:
Here is another UKMT Senior Challenge problem from 2017, which has a straight-forward solution:
“The diagram shows a circle of radius 1 touching three sides of a 2 x 4 rectangle. A diagonal of the rectangle intersects the circle at P and Q, as shown.
What is the length of the chord PQ?
__A_√5____B_4/√5____C_√5 – 2/√5____D_5√5/6____E_2”
See the Circle in Slot Problem for a solution.
 A fun, relatively new, Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos) has puzzles couched in terms of the Holmes-Watson banter. The following problem is a variation on the Sam Loyd Tandem Bicycle Puzzle.
A fun, relatively new, Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos) has puzzles couched in terms of the Holmes-Watson banter. The following problem is a variation on the Sam Loyd Tandem Bicycle Puzzle.
“ ‘Here’s something mostly unrelated for you to chew over, my dear Watson. Say you and I have a single bicycle between us, and no other transport options save walking. We want to get the both of us to a location eighteen miles distant as swiftly as possible. If my walking speed is five miles per hour compared to your four, but for some reason—perhaps a bad ligament—my cycling speed is eight miles per hour compared to your ten. How would you get us simultaneously to our destination with maximum rapidity?’
‘A cab,’ I suggested.
‘Without cheating,’ Holmes replied, and went back to tossing his toast in the air.”
See the Bicycle Problem for solutions.
![]() This is a stimulating little problem from the ever-creative James Tanton:
This is a stimulating little problem from the ever-creative James Tanton:
“An ant is at the east end of an infinite stretchy band, initially 2 ft long. Each day: ant walks 1 ft west on the band. Overnight while sleeping, band stretches to double its length (carrying ant westward as does so). Same routine each day/night. Will ant cover 99% of band’s length?”
(Ant from clipart-library.com)
See the Rubber Band Ant for solutions.
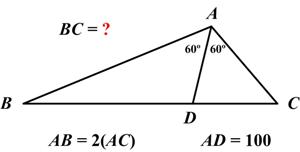 This is another problem from the indefatigable Presh Talwalkar.
This is another problem from the indefatigable Presh Talwalkar.
_ _____Hard Geometry Problem
“In triangle ABC above, angle A is bisected into two 60° angles. If AD = 100, and AB = 2(AC), what is the length of BC?”
See Hard Geometric Problem for solutions.
(Update 7/18/2020, 7/20/2020) Alternative Solution Continue reading
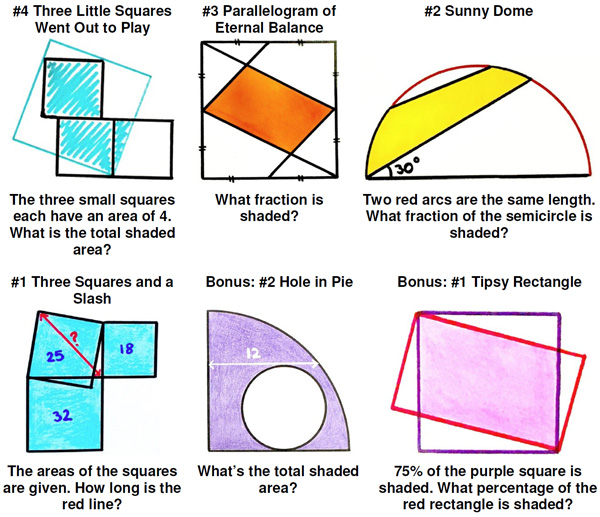
Having fallen under the spell of Catriona Shearer’s geometric puzzles again, I thought I would present the latest group assembled by Ben Orlin, which he dubs “Felt Tip Geometry”, along with a bonus of two more recent ones that caught my fancy as being fine examples of Shearer’s laconic style. Orlin added his own names to the four he assembled and I added names to my two, again ordered from easier to harder.
See Geometric Puzzle Munificence.
(Update 4/16/2020) Ben Orlin has another set of Catriona Shearer puzzles 11 Geometry Puzzles That Drive Mathematicians to Madness which I will leave you to see and enjoy. But I wanted to emphasize some observations he included that I think are spot on. Continue reading
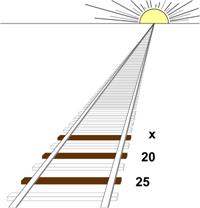 This is a surprisingly challenging puzzle from the Mathematics 2020 calendar.
This is a surprisingly challenging puzzle from the Mathematics 2020 calendar.
“The sketch is of equally spaced railroad ties drawn in a one point perspective. Two of the ties are perceived to the eye to be 25 feet and 20 feet respectively. What is the perceived length x of the third tie?”
Even though the ties are equally-spaced and of equal length in reality, from the point of view of perspective they are successively closer together and diminishing in length. The trick is to figure out what that compression factor is. I had to review my post on the Perspective Map to get some clues.
See the Railroad Tie Problem