 The following puzzle is from the Irishman Owen O’Shea.
The following puzzle is from the Irishman Owen O’Shea.
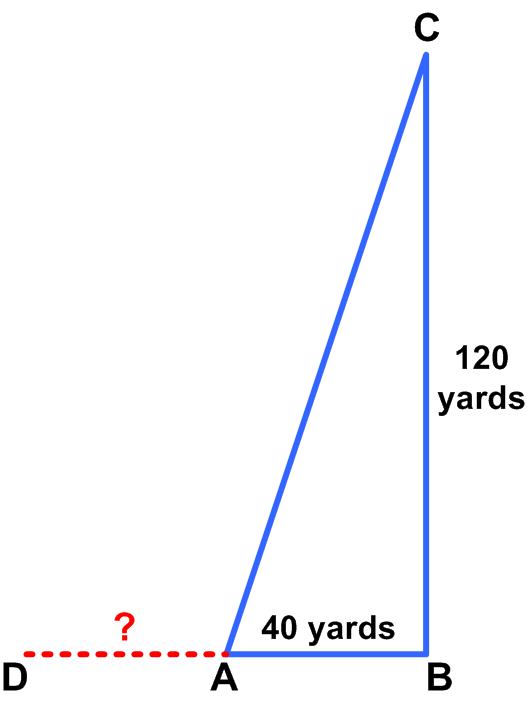
“The figure shows the location of three flags [at A, B, and C] in one of the fields on a neighbor’s farm. The angle ABC is a right angle. Flag A is 40 yards from Flag B. Flag B is 120 yards from flag C. Thus, if one was to walk from A to B and then on to C, one would walk a total of 160 yards.
Now there is a point, marked by flag D, [directly] to the left of flag A. Curiously, if one were to walk from flag A to flag D and then diagonally across to flag C, one would walk a total distance of 160 yards.
The question for our puzzlers is this: how far is it from flag D to flag A?”
This problem has a simple solution. But it also suggests a more advanced alternative approach.
See the Distance to Flag Problem for a solution.

 This is yet another series offered by
This is yet another series offered by 
 This is a slightly different mystery number puzzle from the December 2023
This is a slightly different mystery number puzzle from the December 2023 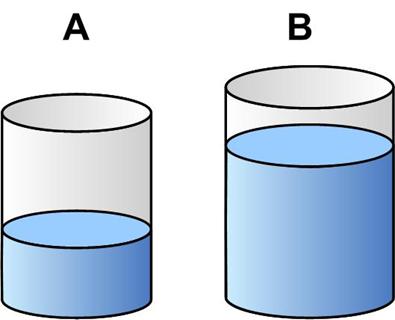 This is a slightly different type of a mixture problem from Dan Griller.
This is a slightly different type of a mixture problem from Dan Griller. This is another race puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings for 2013.
This is another race puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings for 2013.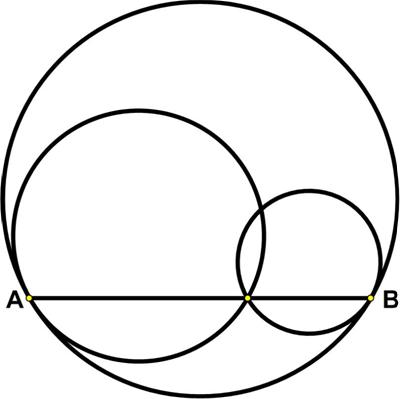 Here is another problem from the “Challenges” section of the Quantum magazine.
Here is another problem from the “Challenges” section of the Quantum magazine.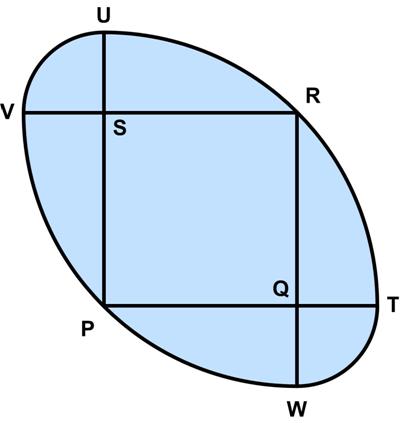 Here is another UKMT Senior Challenge problem for 2017.
Here is another UKMT Senior Challenge problem for 2017.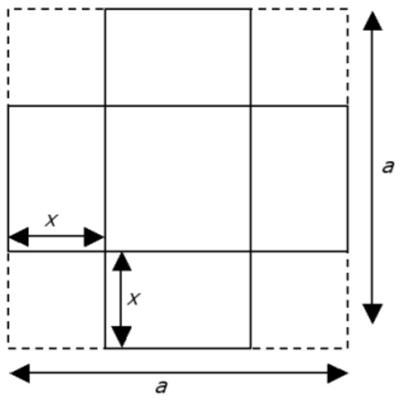 This problem is from Colin Hughes’s Maths Challenge website (mathschallenge.net).
This problem is from Colin Hughes’s Maths Challenge website (mathschallenge.net). Here is another classic example of the three jug problem posed in the Mathigon Puzzle Calendars for 2017.
Here is another classic example of the three jug problem posed in the Mathigon Puzzle Calendars for 2017.