 This is a nice puzzle from Alex Bellos’s Monday Puzzle column in the Guardian.
This is a nice puzzle from Alex Bellos’s Monday Puzzle column in the Guardian.
“My cultural highlight of recent weeks has been the brilliant BBC documentary Gods of Snooker, about the time in the 1980s when the sport was a national obsession. Today’s puzzle describes a shot to malfunction the Romford Robot … and put the Whirlwind … in a spin.
Baize theorem
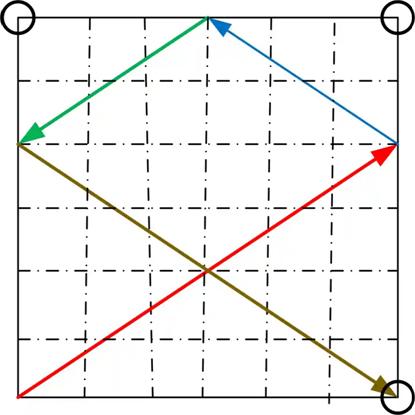
A square snooker table has three corner pockets, as [shown]. A ball is placed at the remaining corner (bottom left). Show that there is no way you can hit the ball so that it returns to its starting position.
The arrows represent one possible shot and how it would rebound around the table.
The table is a mathematical one, which means friction, damping, spin and napping do not exist. In other words, when the ball is hit, it moves in a straight line. The ball changes direction when it bounces off a cushion, with the outgoing angle equal to the incoming angle. The ball and the pockets are infinitely small (i.e. are points), and the ball does not lose momentum, so that its path can include any number of cushion bounces.
Thanks to Dr Pierre Chardaire, associate professor of computing science at the University of East Anglia, who devised today’s puzzle.”
See the Snooker Puzzle

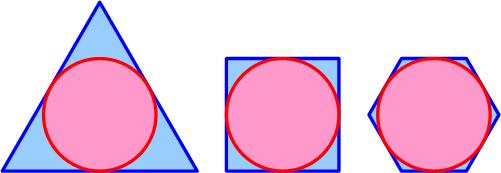 This surprising, but simple, puzzle is from the 12 April MathsMonday
This surprising, but simple, puzzle is from the 12 April MathsMonday 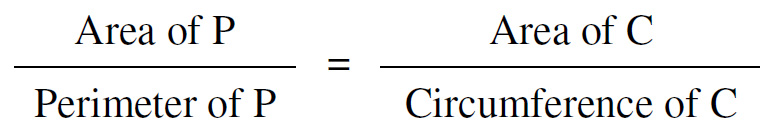
 This is a fairly straight-forward Brainteaser from the Quantum magazine.
This is a fairly straight-forward Brainteaser from the Quantum magazine. I braved another attempt at a Sam Loyd puzzle.
I braved another attempt at a Sam Loyd puzzle.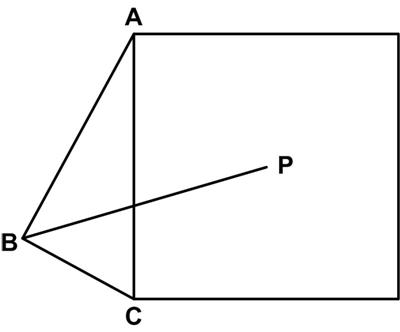 This is a simple problem from Five Hundred Mathematical Challenges:
This is a simple problem from Five Hundred Mathematical Challenges: Here is another, more challenging, problem from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos).
Here is another, more challenging, problem from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos). Futility Closet
Futility Closet The “
The “ Here is a simple problem from an old
Here is a simple problem from an old  This typical problem from the prolific H. E. Dudeney may be a bit tricky at first.
This typical problem from the prolific H. E. Dudeney may be a bit tricky at first.