 This is another doable puzzle from Sam Loyd.
This is another doable puzzle from Sam Loyd.
“BACK OF THE OLDTIME song of “Grandfather’s clock was too tall for the shelf, so it stood for ninety years on the floor,” there was a legend of a pestiferous grand-father and a cantankerous old clock which, from the fitful time when “it was bought on the morn, when the old man was born,” it had made his whole life miserable, owing to an incurable habit which the clock had acquired of getting the hands tangled up whenever they attempted to pass.
These semi-occasional stoppages became of more frequent occurrence as advancing age made the old gentleman more irritable and his feeble hands more incapable of correcting the cranky antics of the balky old timepiece.
Once when the hands came together again and stopped the clock the old man flew into such an ungovernable passion that he fell down in a fit, stone dead, and it was then that
“The clock stopped short,
Never to go again,
When the old man died.”
A photograph of the clock was presented to me, showing the classical figure of a female representing time, and it struck me as remarkable that with the knowledge of the hour and minute hands being together that it should be possible to figure out the exact time at which “the old man died,” from the position of the second hand as shown, without having to see the face of the clock. The idea of being able to figure out the exact time of day from seeing the second hand alone is very odd, although not so difficult a puzzle as one would imagine.”
Answer.
See the Grandfather Clock Puzzle for a solution.
 This problem comes from the Scottish Mathematical Council (SMC) Senior Mathematical Challenge of 2007:
This problem comes from the Scottish Mathematical Council (SMC) Senior Mathematical Challenge of 2007:
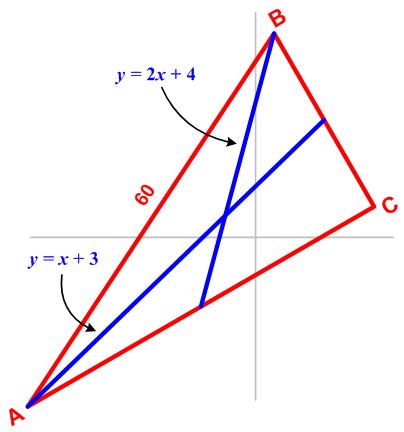 This is a challenging problem from the 1986 American Invitational Mathematics Exam (AIME).
This is a challenging problem from the 1986 American Invitational Mathematics Exam (AIME).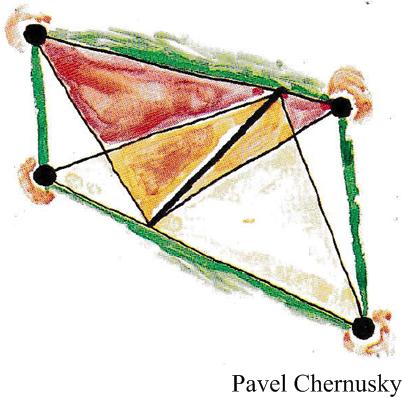 Here is another elegant Quantum math magazine Brainteaser from the imaginative V. Proizvolov.
Here is another elegant Quantum math magazine Brainteaser from the imaginative V. Proizvolov. Here is another logic problem from Ian Stewart.
Here is another logic problem from Ian Stewart.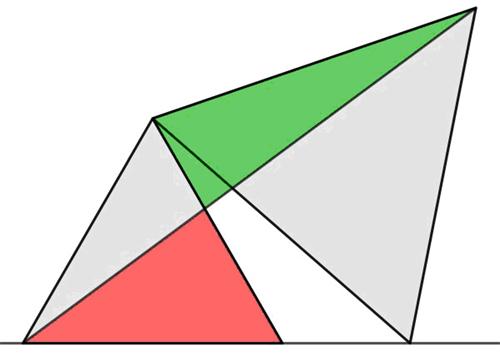 This is a most interesting problem proposed by
This is a most interesting problem proposed by 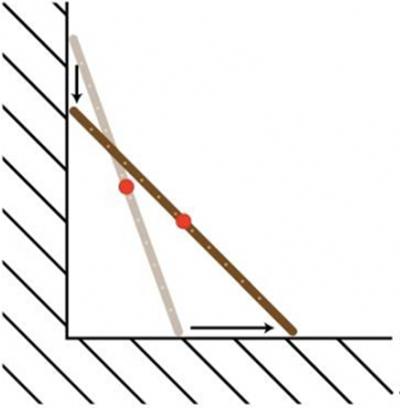 This is a thoughtful puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings.
This is a thoughtful puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings.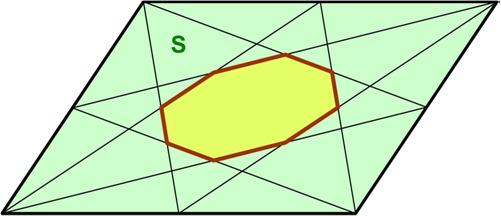 Here is another problem from the Polish Mathematical Olympiads published in 1960.
Here is another problem from the Polish Mathematical Olympiads published in 1960.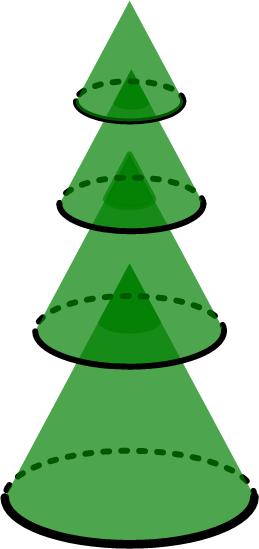 This is a belated Christmas puzzle from December 2019
This is a belated Christmas puzzle from December 2019  Here is another sum problem, this time from the 2021 Math Calendar.
Here is another sum problem, this time from the 2021 Math Calendar. This is another doable puzzle from Sam Loyd.
This is another doable puzzle from Sam Loyd.