 This is a logical puzzle from Muhammad Zain Sarwar on Puzzle Sphere.
This is a logical puzzle from Muhammad Zain Sarwar on Puzzle Sphere.
“Real Psychological Puzzle that will Test your Logical Thinking
Only 10% of Participants gave the Right Answer!
Imagine in front of you there are four cards placed on a desk. Each card has a number on one side and a color on the other. The visible faces of the cards show the following:
You are given a rule to verify:
“Every card that shows an even number on one side, then the opposite side must be red.”
Puzzle Statement
Your task is to determine which cards you must flip over to check whether this rule is being followed or not.
This question was part of a real psychological experiment.”
(I emphasized the “must” in the puzzle statement in order to limit the number of cards flipped to the minimum.)
See Logical Card Test for a solution.
Post Views: 261
 This is another problem from A+Click.
This is another problem from A+Click.
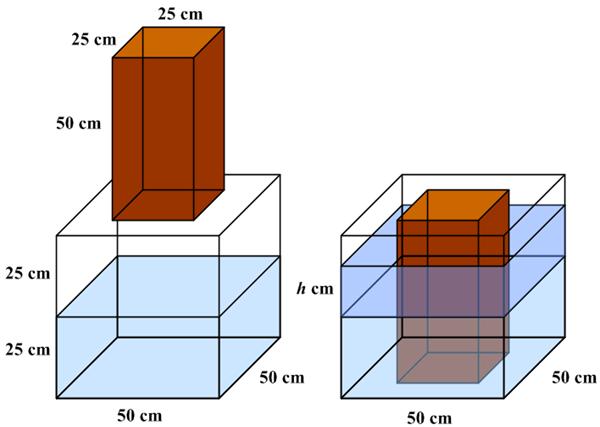 I thought this puzzle, which was included among a set of seven
I thought this puzzle, which was included among a set of seven  This is another challenging sum from the 2024 Math Calendar.
This is another challenging sum from the 2024 Math Calendar.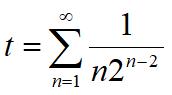 ”
” Continuing the logic thread, this is a nice logic
Continuing the logic thread, this is a nice logic  This is a logical
This is a logical 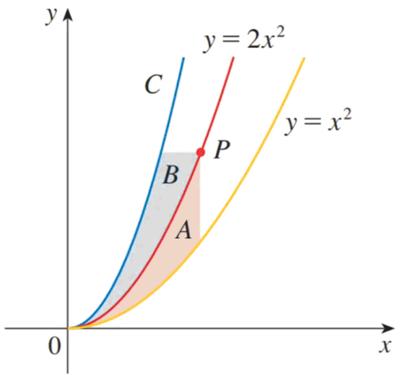 Here is another
Here is another  Here is an entertaining
Here is an entertaining 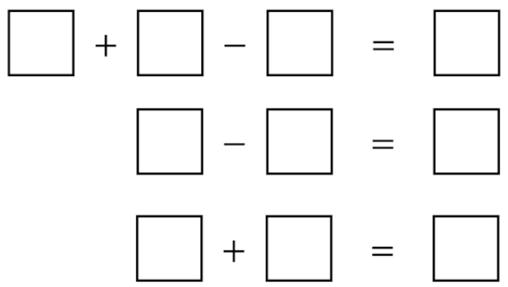 This is a somewhat unusual
This is a somewhat unusual  On March 7 one of my favorite bloggers, Kevin Drum,
On March 7 one of my favorite bloggers, Kevin Drum, 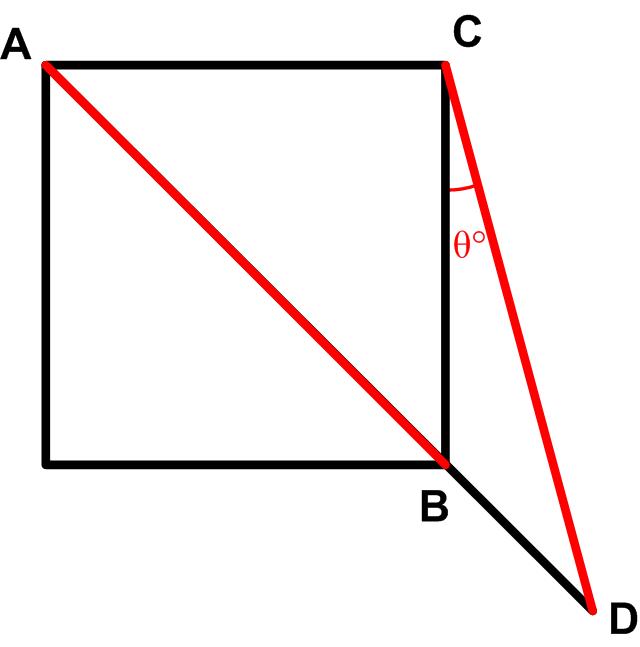 For me this turned out to be sort of a challenging problem from the 2025 Math Calendar.
For me this turned out to be sort of a challenging problem from the 2025 Math Calendar.