 The following puzzle is from the Irishman Owen O’Shea.
The following puzzle is from the Irishman Owen O’Shea.
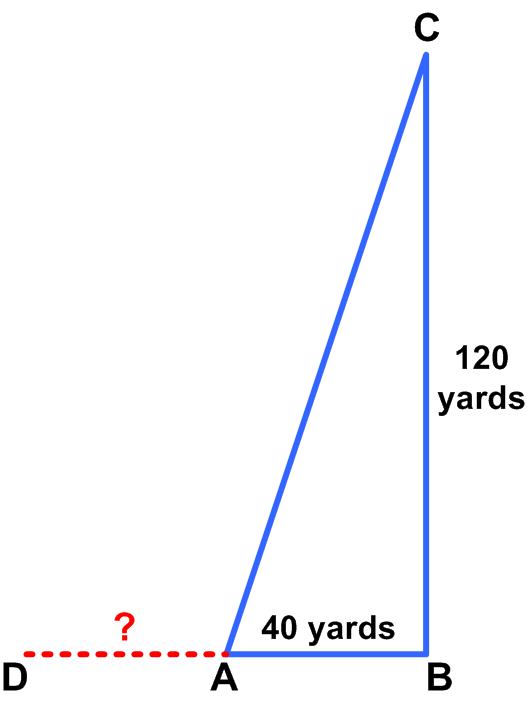
“The figure shows the location of three flags [at A, B, and C] in one of the fields on a neighbor’s farm. The angle ABC is a right angle. Flag A is 40 yards from Flag B. Flag B is 120 yards from flag C. Thus, if one was to walk from A to B and then on to C, one would walk a total of 160 yards.
Now there is a point, marked by flag D, [directly] to the left of flag A. Curiously, if one were to walk from flag A to flag D and then diagonally across to flag C, one would walk a total distance of 160 yards.
The question for our puzzlers is this: how far is it from flag D to flag A?”
This problem has a simple solution. But it also suggests a more advanced alternative approach.
Answer.
See the Distance to Flag Problem for a solution.
Post Views: 311
 Here is a fairly computationally challenging 1994 AIME problem .
Here is a fairly computationally challenging 1994 AIME problem .
 My cousin sent me this
My cousin sent me this  Well, I discovered that the 2024 Math Calendar has some interesting problems, so I guess things will limp along for a while. This is a challenging but imaginative problem from the calendar.
Well, I discovered that the 2024 Math Calendar has some interesting problems, so I guess things will limp along for a while. This is a challenging but imaginative problem from the calendar.
 So I managed to make it five years. Again, I thought I would present the statistical pattern of interaction with the website in the absence of any explicit feedback.
So I managed to make it five years. Again, I thought I would present the statistical pattern of interaction with the website in the absence of any explicit feedback. The following puzzle is from the Irishman Owen O’Shea.
The following puzzle is from the Irishman Owen O’Shea.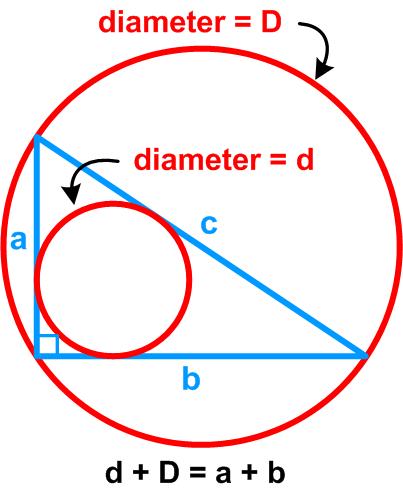
 This is yet another series offered by
This is yet another series offered by 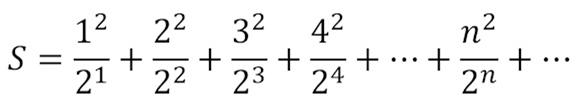
 This is a slightly different mystery number puzzle from the December 2023
This is a slightly different mystery number puzzle from the December 2023  This is a slightly different type of a mixture problem from Dan Griller.
This is a slightly different type of a mixture problem from Dan Griller. This is another race puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings for 2013.
This is another race puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings for 2013.