 This is a most surprising and amazing identity from the 1965 Polish Mathematical Olympiads.
This is a most surprising and amazing identity from the 1965 Polish Mathematical Olympiads.
“31. Prove that if n is a natural number, then we have
(√2 – 1)n = √m – √(m – 1),
where m is a natural number.”
Here, natural numbers are 1, 2, 3, …
I found it to be quite challenging, as all the Polish Math Olympiad problems seem to be.
See the Amazing Identity

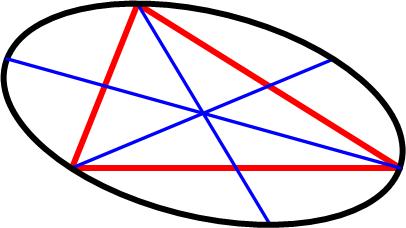 This is a tantalizing problem from the 1977 Crux Mathematicorum.
This is a tantalizing problem from the 1977 Crux Mathematicorum. This is a somewhat challenging problem from the 1997 American Invitational Mathematics Exam (AIME).
This is a somewhat challenging problem from the 1997 American Invitational Mathematics Exam (AIME).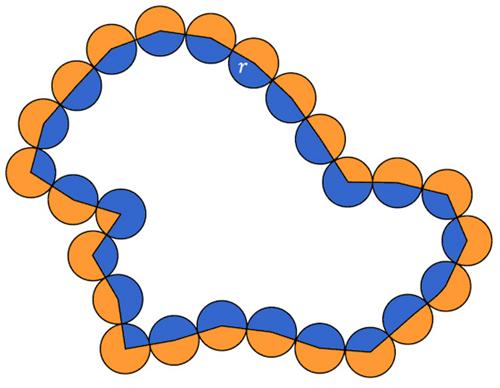 This is a nifty
This is a nifty  This is a fairly extensive clock problem by Geoffrey Mott-Smith from 1954.
This is a fairly extensive clock problem by Geoffrey Mott-Smith from 1954. This is a slightly challenging problem from Dan Griller.
This is a slightly challenging problem from Dan Griller.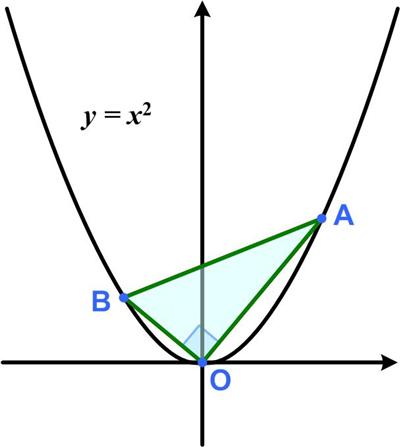 Since the changes in Twitter (now X), I have not been able to see the posts, not being a subscriber. But I noticed poking around that some twitter accounts were still viewable. However, like some demented aging octogenarian they had lost track of time, that is, instead of being sorted with the most recent post first, they showed a random scattering of posts from different times. So a current post could be right next to one several years ago. That is what I discovered with the now defunct MathsMonday site. I found a
Since the changes in Twitter (now X), I have not been able to see the posts, not being a subscriber. But I noticed poking around that some twitter accounts were still viewable. However, like some demented aging octogenarian they had lost track of time, that is, instead of being sorted with the most recent post first, they showed a random scattering of posts from different times. So a current post could be right next to one several years ago. That is what I discovered with the now defunct MathsMonday site. I found a  This essay is slightly tangential to my usual fare, but it is prompted by a most amazing video that convinced me that the impact of AI this time is not hype, but rather a real threat to our society. I found the
This essay is slightly tangential to my usual fare, but it is prompted by a most amazing video that convinced me that the impact of AI this time is not hype, but rather a real threat to our society. I found the 
 This is another puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings.
This is another puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings.