 This is a straight-forward problem from Geoffrey Mott-Smith in 1954.
This is a straight-forward problem from Geoffrey Mott-Smith in 1954.
“A brown Terraplane car whizzed past the State Police booth, going 80 miles per hour. The trooper on duty phoned an alert to other stations on the road, then set out on his motorcycle in pursuit. He had gone only a short distance when the brown Terraplane hurtled past him, going in the opposite direction. The car was later caught by a road block, and its occupants proved to be a gang of thieves who had just robbed a jewelry store.
Witnesses testified that the thieves had put their plunder in the car when they fled the scene of the crime. But it was no longer in the car when it was caught. Reports on the wild ride showed that the only time the car could have stopped was in doubling back past the State Police booth.
The trooper reported that the point at which the car passed him on its return was just 2 miles from his booth, and that it reached him just 7 minutes after it had first passed his booth. On both occasions it was apparently making its top speed of 80 miles per hour.
The investigators assumed that the car had made a stop and turned around while some members of the gang cached the loot by the roadside, or perhaps at the office of a “fence.” In an effort to locate the cache, they assumed that the car had maintained a uniform speed, and allowed 2 minutes as the probable loss of time in bringing the car to a halt, turning it, and regaining full speed.
On this assumption, what was the farthest point from the booth that would have to be covered by the search for the loot?”
Answer.
See Locating the Loot for solutions.
Post Views: 186
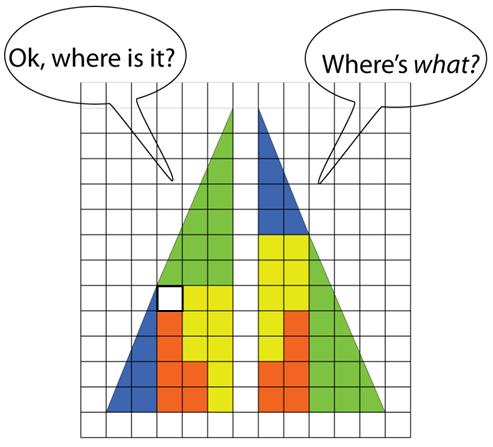 Coming across this classic geometric paradox recently in Futility Closet motivated me to write down its solution in detail.
Coming across this classic geometric paradox recently in Futility Closet motivated me to write down its solution in detail.
 This is a clever puzzle from the 1986 AIME problems.
This is a clever puzzle from the 1986 AIME problems. This is an intriguing
This is an intriguing 
 In one of our periodic FaceTime calls I found out that my granddaughter in 6th grade was interested in learning algebra and had gotten a book to help her out. Clearly this initiative to get a head start prior to the normal course curriculum excited me, so I wrote what I thought was an insightful essay on the meaning and purpose of algebra. Needless to say it was an abysmal failure.
In one of our periodic FaceTime calls I found out that my granddaughter in 6th grade was interested in learning algebra and had gotten a book to help her out. Clearly this initiative to get a head start prior to the normal course curriculum excited me, so I wrote what I thought was an insightful essay on the meaning and purpose of algebra. Needless to say it was an abysmal failure. The following is another puzzle from the Irishman Owen O’Shea.
The following is another puzzle from the Irishman Owen O’Shea. This is a straight-forward problem from Geoffrey Mott-Smith in 1954.
This is a straight-forward problem from Geoffrey Mott-Smith in 1954.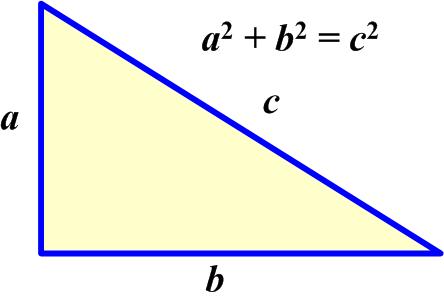 One of the joys of getting old is that you forget things. So one of the things I recall is that the converse of the Pythagorean Theorem is true, that is, if a triangle with short sides a and b and long side c is such that
One of the joys of getting old is that you forget things. So one of the things I recall is that the converse of the Pythagorean Theorem is true, that is, if a triangle with short sides a and b and long side c is such that This is a relatively simple probability
This is a relatively simple probability  This is a recent Alex Bellos
This is a recent Alex Bellos  One is reduced to hysterical laughter to try to maintain a modicum of sanity.
One is reduced to hysterical laughter to try to maintain a modicum of sanity.