 This is a classic puzzle from Presh Talwalkar.
This is a classic puzzle from Presh Talwalkar.
“This puzzle has been asked as an interview question at tech companies like Google.
There are 100 lights numbered 1 to 100, all starting in the off position. There are also 100 people numbered 1 to 100. First, person 1 toggles every light switch (toggle means to change from off to on, or change from on to off). Then person 2 toggles every 2nd light switch, and so on, where person i toggles every ith light switch. The last person is person 100 who toggles every 100th switch.
After all 100 people have passed, which light bulbs will be turned on?”
I vaguely remembered the answer, which I confirmed after a few examples. But I didn’t remember an exact proof, so I thought I would give it a try.
See 100 Light Bulbs Puzzle for solutions.

 This
This 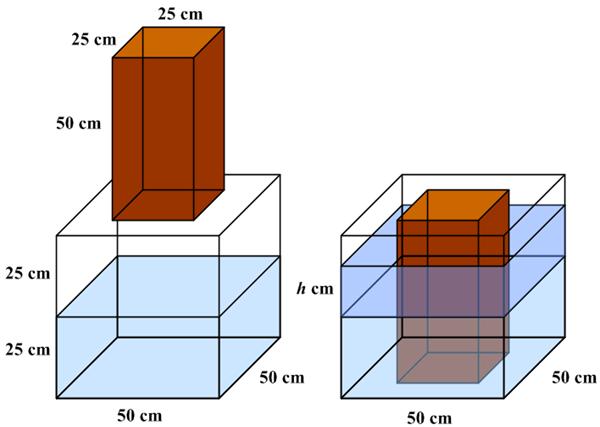 I thought this puzzle, which was included among a set of seven
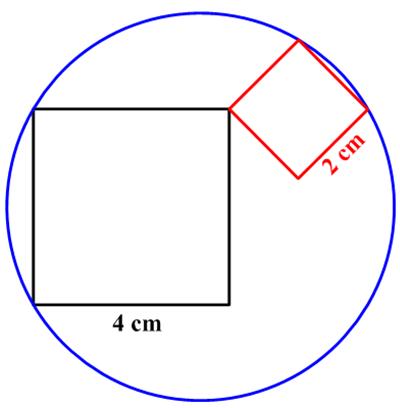
I thought this puzzle, which was included among a set of seven 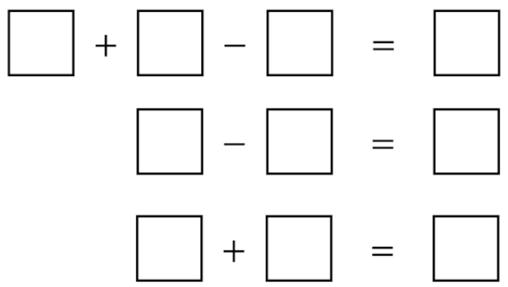 This is a somewhat unusual
This is a somewhat unusual 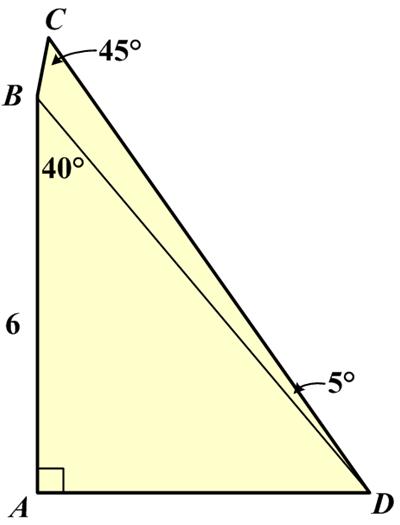 This is another intimidating
This is another intimidating  Presh Talwalkar has an interesting new
Presh Talwalkar has an interesting new 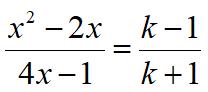 ”
” Presh Talwalkar presented an interesting puzzle that originated in the Ladies’ Diary of 1739-40, was recast by Henry Dudeney in 1917, and further modified using American money.
Presh Talwalkar presented an interesting puzzle that originated in the Ladies’ Diary of 1739-40, was recast by Henry Dudeney in 1917, and further modified using American money. This is a relatively simple probability
This is a relatively simple probability  This is yet another series offered by
This is yet another series offered by 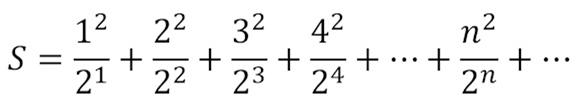
 This is a nifty
This is a nifty