 Yet another interesting problem from Presh Talwalkar.
Yet another interesting problem from Presh Talwalkar.
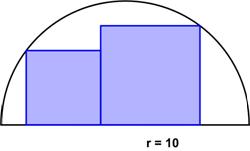
“Two side-by-side squares are inscribed in a semicircle. If the semicircle has a radius of 10, can you solve for the total area of the two squares? If no, demonstrate why not. If yes, calculate the answer.”
This puzzle shares the characteristics of all good problems where the information provided seems insufficient.
See the Sum of Squares Puzzle for solutions.

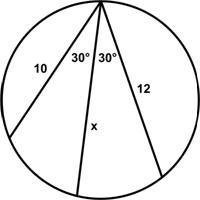 This is another challenging puzzle from
This is another challenging puzzle from 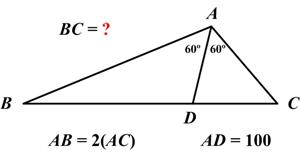 This is another problem from the indefatigable Presh Talwalkar.
This is another problem from the indefatigable Presh Talwalkar.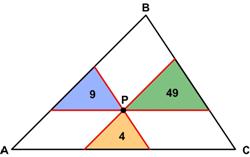 Here is another engaging problem from
Here is another engaging problem from 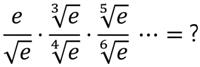 This is a delightful and surprising problem from
This is a delightful and surprising problem from 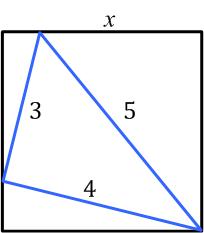 Presh Talwalkar had another interesting
Presh Talwalkar had another interesting  This is another intriguing problem from Presh Talwalkar.
This is another intriguing problem from Presh Talwalkar.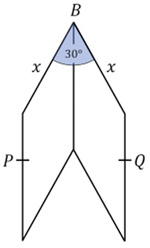 Another challenging problem from
Another challenging problem from 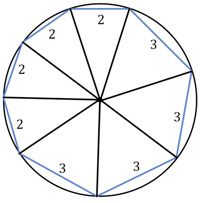 Here is a problem from the famous (infamous?) Putnam exam, presented by Presh Talwalkar. Needless to say, I did not solve it in 30 minutes—but at least I solved it (after making a blizzard of arithmetic and trigonometric errors).
Here is a problem from the famous (infamous?) Putnam exam, presented by Presh Talwalkar. Needless to say, I did not solve it in 30 minutes—but at least I solved it (after making a blizzard of arithmetic and trigonometric errors).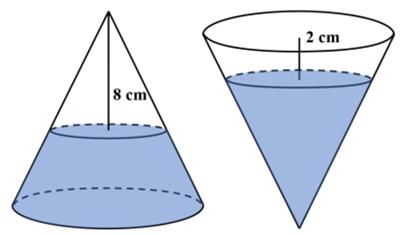 I was astonished that this problem was suitable for 8th graders. First of all the formula for the volume of a cone is one of the least-remembered of formulas, and I certainly never remember it. So my only viable approach was calculus, which is probably not a suitable solution for an 8th grader.
I was astonished that this problem was suitable for 8th graders. First of all the formula for the volume of a cone is one of the least-remembered of formulas, and I certainly never remember it. So my only viable approach was calculus, which is probably not a suitable solution for an 8th grader.