 Here is a seemingly simple problem from Futility Closet.
Here is a seemingly simple problem from Futility Closet.
“A quickie from Peter Winkler’s Mathematical Puzzles, 2021: Can West Virginia be inscribed in a square? That is, is it possible to draw some square each of whose four sides is tangent to this shape?”
Technically we might rephrase this as, can we inscribe a flat map of West Virginia in a square, since the boundary of most states is probably not differentiable everywhere, that is, has a tangent everywhere.
But the real significance of the problem is that it is an example of an “existence proof”, which in mathematics refers to a proof that asserts the existence of a solution to a problem, but does not (or cannot) produce the solution itself. These proofs are second in delight only to the “impossible proofs” which prove that something is impossible, such as trisecting an angle solely with ruler and compass.
Here is another classic example (whose origin I don’t recall). Consider the temperatures of the earth around the equator. At any given instant of time there must be at least two antipodal points that have the same temperature. (Antipodal points are the opposite ends of a diameter through the center of the earth.)
See Existence Proofs (revised)
(Update 10/2/2021) I fixed a minor typo: “tail” should have been “head”
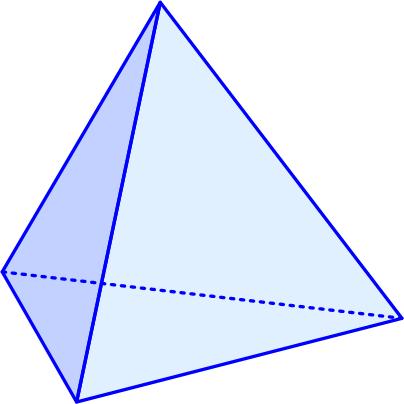 Futility Closet has another example of an existence proof like their previous one taken from Peter Winkler’s 2021 Mathematical Puzzles (see my post “Existence Proofs”):
Futility Closet has another example of an existence proof like their previous one taken from Peter Winkler’s 2021 Mathematical Puzzles (see my post “Existence Proofs”):
 Here is a seemingly simple problem from Futility Closet.
Here is a seemingly simple problem from Futility Closet.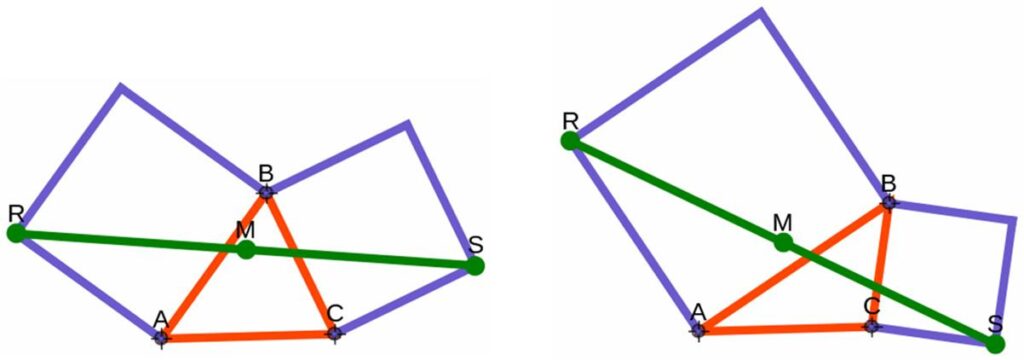
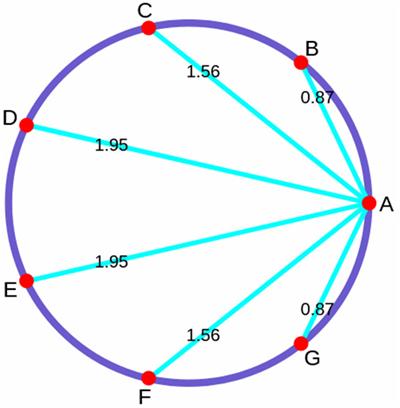 Futility Closet
Futility Closet Here is a simple problem from an old
Here is a simple problem from an old 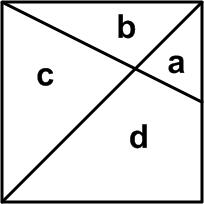 Here is a simple Futility Closet problem from 2014.
Here is a simple Futility Closet problem from 2014. Here is a nice logic puzzle from 2014 Futility Closet.
Here is a nice logic puzzle from 2014 Futility Closet.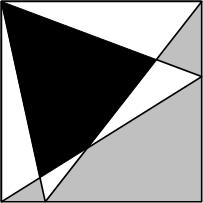 This is a problem from a while back (2015) at Futility Closet.
This is a problem from a while back (2015) at Futility Closet.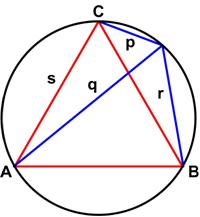 This is another fairly simple puzzle from Futility Closet.
This is another fairly simple puzzle from Futility Closet.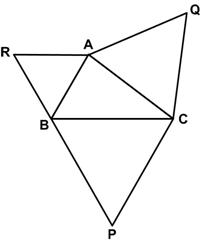 Here is another simple problem from Futility Closet.
Here is another simple problem from Futility Closet.