 This statement showed up recently at Futility Closet and I found it to be another one of those magical results that seemed so surprising. I don’t recall ever seeing this before.
This statement showed up recently at Futility Closet and I found it to be another one of those magical results that seemed so surprising. I don’t recall ever seeing this before.
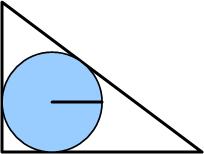
“The radius of a circle inscribed in a 3-4-5 triangle is 1.
(In fact, the inradius of any Pythagorean triangle is an integer.)”
(A Pythagorean triangle is a right triangle whose sides form a Pythagorean triple.) Futility Closet left these remarkable statements unproven, so naturally I felt I had to provide a proof.

 Futility Closet presented a nifty method of solving the “counterfeit coin in 12 coins” problem in a way I had not seen before by mapping the problem into numbers in base 3. It wasn’t immediately clear to me how their solution worked, so I decided to write up my own explanation.
Futility Closet presented a nifty method of solving the “counterfeit coin in 12 coins” problem in a way I had not seen before by mapping the problem into numbers in base 3. It wasn’t immediately clear to me how their solution worked, so I decided to write up my own explanation.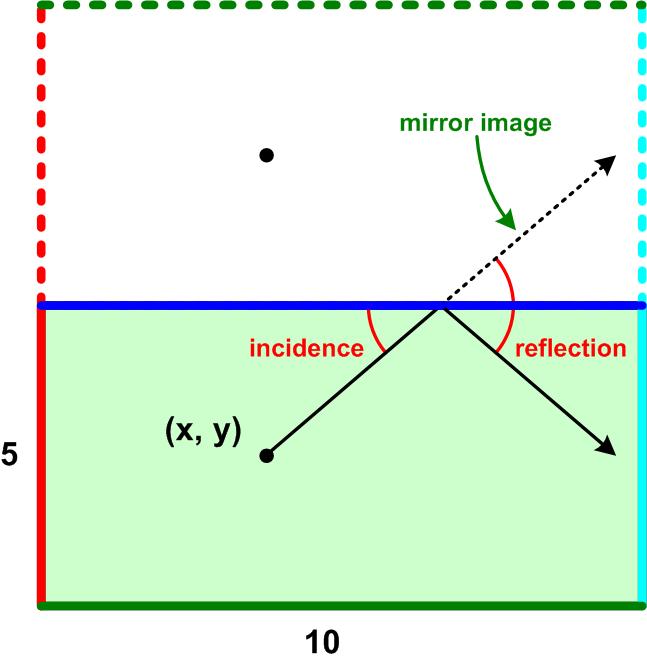 Futility Closet offers another interesting puzzle:
Futility Closet offers another interesting puzzle: This problem from
This problem from 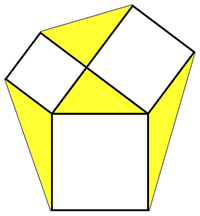 From
From 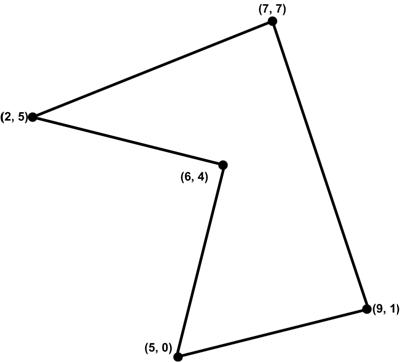 This is another problem from
This is another problem from 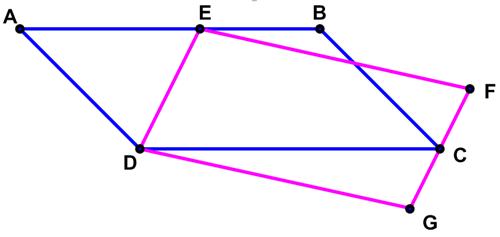 Yet another
Yet another 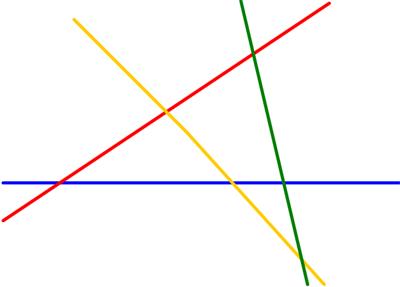 This is another
This is another 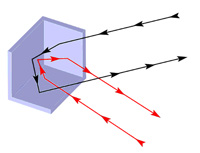 I came across the following entry in the
I came across the following entry in the