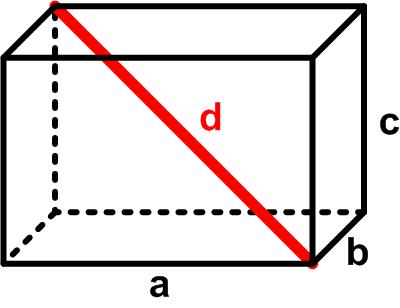
 This is a slightly stimulating thought puzzle from Futility Closet.
This is a slightly stimulating thought puzzle from Futility Closet.
“You have three identical bricks and a ruler. How can you determine the length of a brick’s interior diagonal without any calculation?”
See A Simple Plan

 This is a slightly stimulating thought puzzle from Futility Closet.
This is a slightly stimulating thought puzzle from Futility Closet.
“You have three identical bricks and a ruler. How can you determine the length of a brick’s interior diagonal without any calculation?”
See A Simple Plan
 This is a lovely result from Futility Closet.
This is a lovely result from Futility Closet.
“Draw an arbitrary quadrilateral and divide each of its sides into three equal parts. Draw a line through adjacent points of trisection on either side of each vertex and you’ll have a parallelogram.
Discovered by Austrian engineer Ferdinand Wittenbauer.”
Find a proof.
See Wittenbauer’s Parallelogram for a solution.
 Here is an entertaining puzzle from Futility Closet.
Here is an entertaining puzzle from Futility Closet.
“By Wikimedia user Efbrazil. Begin at the star. The number at your current position tells you the number of blocks that your next jump must span. All jumps must be orthogonal. So, for example, your first jump must take you to the 1 in the lower left corner or the 2 in the upper right. What sequence of jumps will return you to the star?”
See A Number Maze for solutions
 This is a puzzle from Futility Closet.
This is a puzzle from Futility Closet.
“A puzzle by Steven T., a systems engineer at the National Security Agency, from the NSA’s September 2016 Puzzle Periodical:
Three athletes (and only three athletes) participate in a series of track and field events. Points are awarded for 1st, 2nd, and 3rd place in each event (the same points for each event, i.e. 1st always gets “x” points, 2nd always gets “y” points, 3rd always gets “z” points), with x > y > z > 0, and all point values being integers.
The athletes are named Adam, Bob, and Charlie.
Question: Who finished second in the 100-meter dash (and why)?”
I thought this puzzle impossible at first. There didn’t seem to be enough information to solve it. But a bit of trial-and-error opened a path.
See NSA Track and Field Puzzle for solutions.
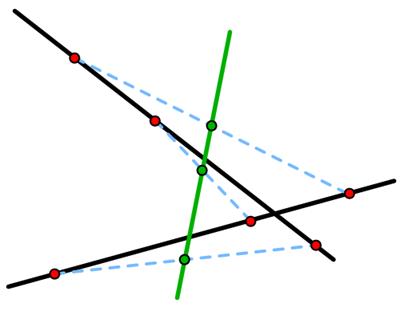 I came across this remarkable result in Futility Closet:
I came across this remarkable result in Futility Closet:
“On each of these two black lines is a trio of red points marked by the same distances. The midpoints of segments drawn between corresponding points are collinear.
(Discovered by Danish mathematician Johannes Hjelmslev.)”
This result seems amazing and mysterious. I wondered if I could think of a proof. I found a simple approach that did not use plane geometry. And suddenly, like a magic trick exposed, the result seemed obvious.
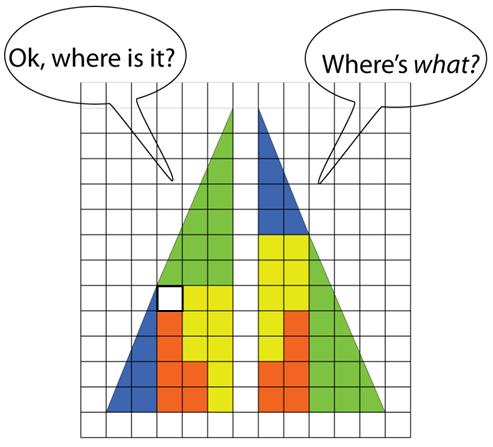 Coming across this classic geometric paradox recently in Futility Closet motivated me to write down its solution in detail.
Coming across this classic geometric paradox recently in Futility Closet motivated me to write down its solution in detail.
“Where did the empty square come from?”
In any case, this is the canonical example for why I avoid visual geometric proofs—you can be so easily fooled. Real proofs require plane or analytic geometry arguments.
See the Classic Geometry Paradox
(Update 9/14/2024) Penn & Teller – Fool Us – Magic Trick
Continue reading
 This is an intriguing puzzle from Futility Closet.
This is an intriguing puzzle from Futility Closet.
“In Robert Chambers’ 1906 novel The Tracer of Lost Persons, Mr. Keen copies the figure below from a mysterious photograph. He is trying to help Captain Harren find a young woman with whom he has become obsessed.
‘It’s the strangest cipher I ever encountered,’ he says at length. ‘The strangest I ever heard of. I have seen hundreds of ciphers—hundreds—secret codes of the State Department, secret military codes, elaborate Oriental ciphers, symbols used in commercial transactions, symbols used by criminals and every species of malefactor. And every one of them can be solved with time and patience and a little knowledge of the subject. But this … this is too simple.’
The message reveals the name of the young woman whom Captain Harren has been seeking. What is it?”
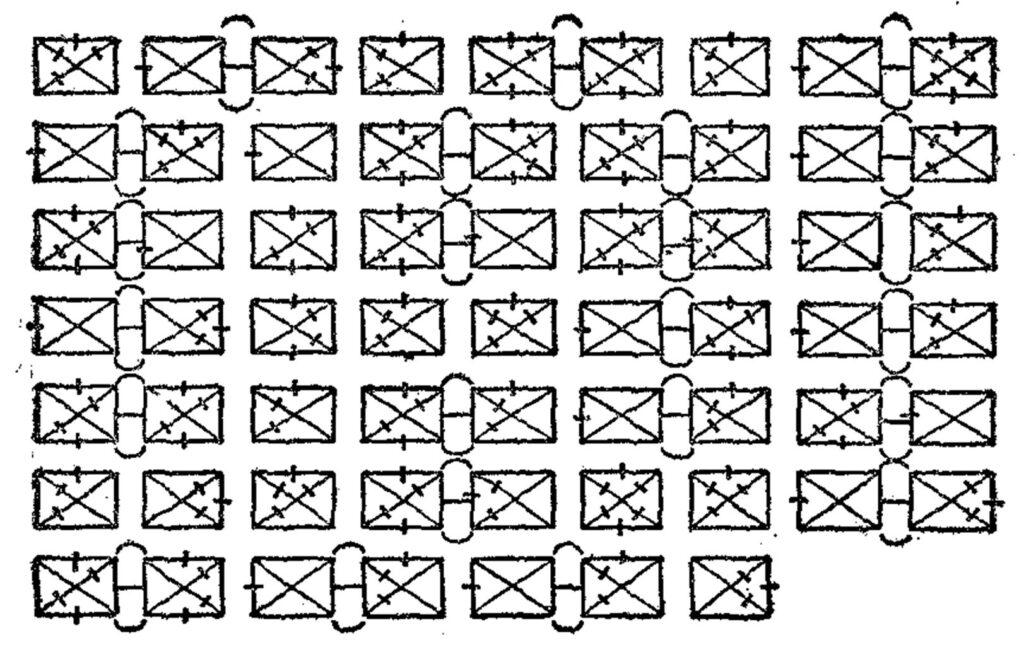
As is usual with these types of puzzles, I felt foolish that I couldn’t see the immediate, simple interpretation of the boxes—after a great deal of effort. So I solved it using the usual cryptographic methods that rely heavily on logic and letter frequencies, though the message is a bit short for that.
See Box Code Puzzle for solutions.
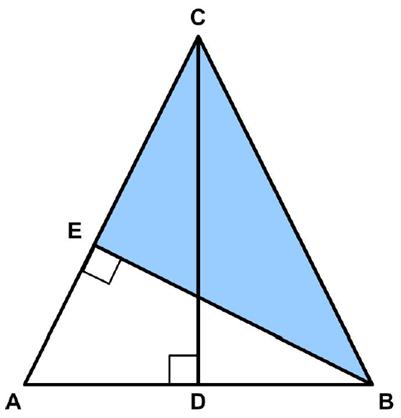 The Futility Closet website had the following problem:
The Futility Closet website had the following problem:
“In isosceles triangle ABC, CD = AB and BE is perpendicular to AC. Show that CEB is a 3-4-5 right triangle.”
See a Triangle Puzzle
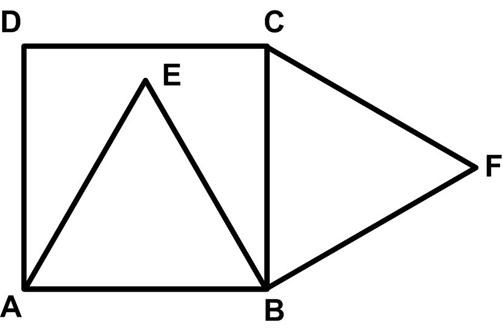 This is a fairly simple problem from Futility Closet, which is currently under a hiatus.
This is a fairly simple problem from Futility Closet, which is currently under a hiatus.
“Robert Bilinski proposed this problem in the April 2006 issue of Crux Mathematicorum. On square ABCD, two equilateral triangles are constructed, ABE internally and BCF externally, as shown. Prove that D, E, and F are collinear.”
See Line Work

Here is a mind-numbing logic puzzle from Futility Closet.
“A puzzle by H.A. Thurston, from the April 1947 issue of Eureka, the journal of recreational mathematics published at Cambridge University:
Five people make the following statements:—

Which of these statements are true and which false? It will be found on trial that there is only one possibility. Thus, prove or disprove Fermat’s last theorem.”
Normally I would forgo something this complicated, but I thought I would give it a try. I was surprised that I was able to solve it, though it took some tedious work. (Hint: truth tables. See the “Pointing Fingers” post regarding truth tables.)
One important note. The author is a bit cavalier about the use of “Either …, or …”. In common parlance this means “either P is true or Q is true, but not both” (exclusive “or”: XOR), whereas in logic “or” means “either P is true or Q is true, or possibly both” (inclusive “or”: OR). I assumed all “Either …, or …” and “or” expressions were the logical inclusive “or”, which turned out to be the case.
See the Fermat’s Last Theorem Puzzle