 Futility Closet presented a nifty method of solving the “counterfeit coin in 12 coins” problem in a way I had not seen before by mapping the problem into numbers in base 3. It wasn’t immediately clear to me how their solution worked, so I decided to write up my own explanation.
Futility Closet presented a nifty method of solving the “counterfeit coin in 12 coins” problem in a way I had not seen before by mapping the problem into numbers in base 3. It wasn’t immediately clear to me how their solution worked, so I decided to write up my own explanation.
Futility Closet: “You have 12 coins that appear identical. Eleven have the same weight, but one is either heavier or lighter than the others. How can you identify it, and determine whether it’s heavy or light, in just three weighings in a balance scale? This is a classic puzzle, but in 1992 Washington State University mathematician Calvin T. Long found a solution ‘that appears little short of magic.’ ”
See Counterfeit Coin in Base 3.
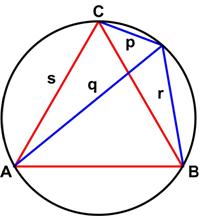 This is another fairly simple puzzle from Futility Closet.
This is another fairly simple puzzle from Futility Closet.
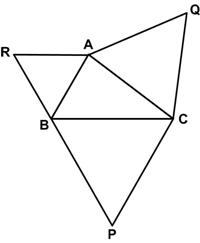 Here is another simple problem from Futility Closet.
Here is another simple problem from Futility Closet.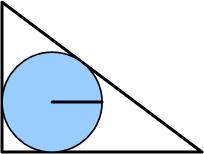 This statement showed up recently at
This statement showed up recently at 
 Futility Closet presented a nifty method of solving the “counterfeit coin in 12 coins” problem in a way I had not seen before by mapping the problem into numbers in base 3. It wasn’t immediately clear to me how their solution worked, so I decided to write up my own explanation.
Futility Closet presented a nifty method of solving the “counterfeit coin in 12 coins” problem in a way I had not seen before by mapping the problem into numbers in base 3. It wasn’t immediately clear to me how their solution worked, so I decided to write up my own explanation. Futility Closet offers another interesting puzzle:
Futility Closet offers another interesting puzzle: This problem from
This problem from  From
From 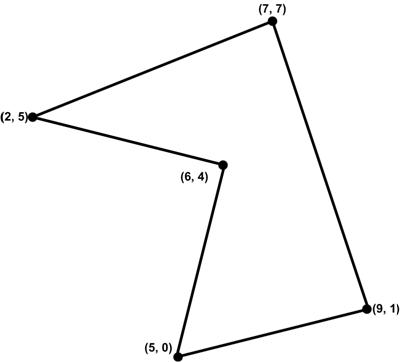 This is another problem from
This is another problem from  Yet another
Yet another