 I think this turned out to be an even trickier problem than Alex Bellos thought.
I think this turned out to be an even trickier problem than Alex Bellos thought.
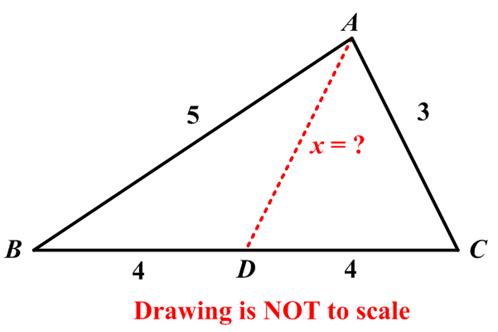
“Tricky triangle This one was sent in by a reader, aged 85, who first saw it in 1960. He is a roboticist who passed through Harvard, Princeton, Stanford and IBM. He says it is his favourite puzzle. ‘I’ve given this puzzle to perhaps 100 people. Over 80% have no idea how to solve it.’ What is the length of AD, the dashed line?”
See Tricky Triangle for solutions.

 This is another
This is another 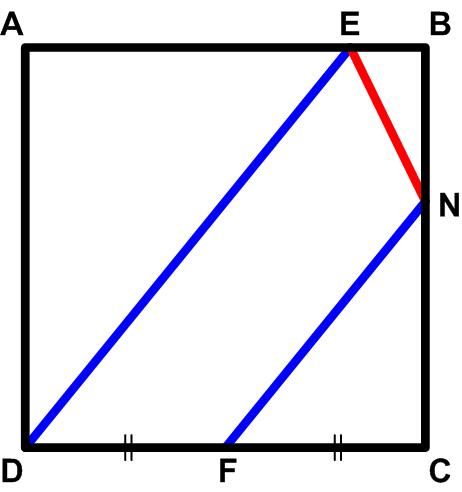 This is an interesting problem from the collection Five Hundred Mathematical Challenges.
This is an interesting problem from the collection Five Hundred Mathematical Challenges. I came across this remarkable
I came across this remarkable 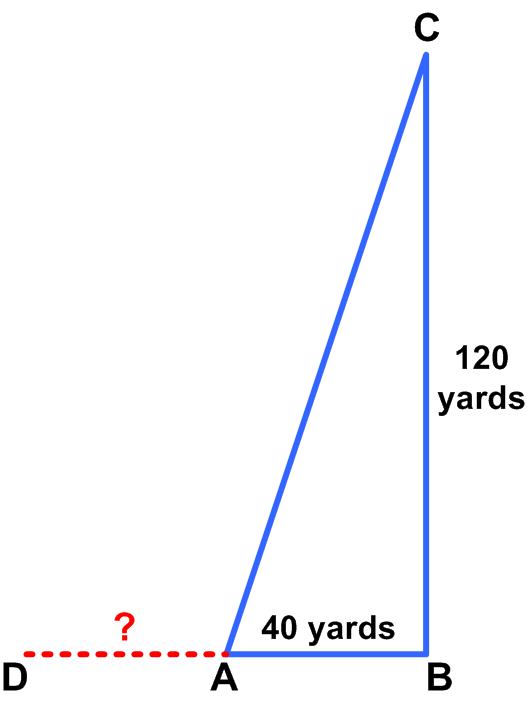 The following puzzle is from the Irishman Owen O’Shea.
The following puzzle is from the Irishman Owen O’Shea.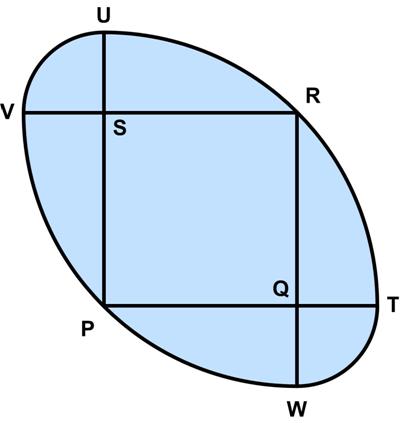 Here is another UKMT Senior Challenge problem for 2017.
Here is another UKMT Senior Challenge problem for 2017.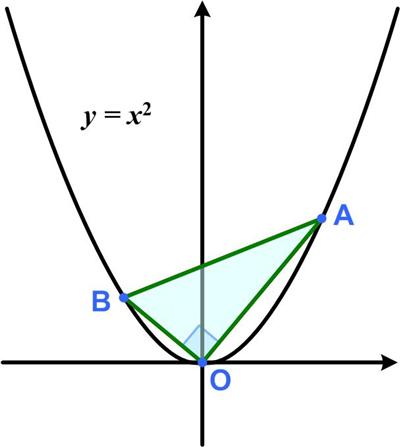 Since the changes in Twitter (now X), I have not been able to see the posts, not being a subscriber. But I noticed poking around that some twitter accounts were still viewable. However, like some demented aging octogenarian they had lost track of time, that is, instead of being sorted with the most recent post first, they showed a random scattering of posts from different times. So a current post could be right next to one several years ago. That is what I discovered with the now defunct MathsMonday site. I found a
Since the changes in Twitter (now X), I have not been able to see the posts, not being a subscriber. But I noticed poking around that some twitter accounts were still viewable. However, like some demented aging octogenarian they had lost track of time, that is, instead of being sorted with the most recent post first, they showed a random scattering of posts from different times. So a current post could be right next to one several years ago. That is what I discovered with the now defunct MathsMonday site. I found a 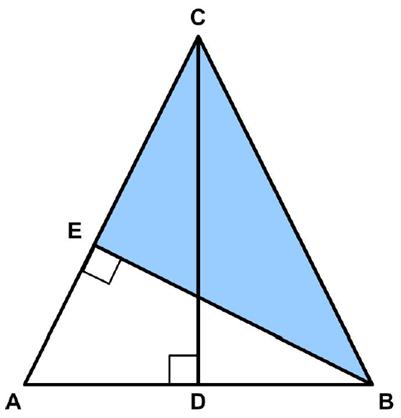 The Futility Closet website had the following
The Futility Closet website had the following 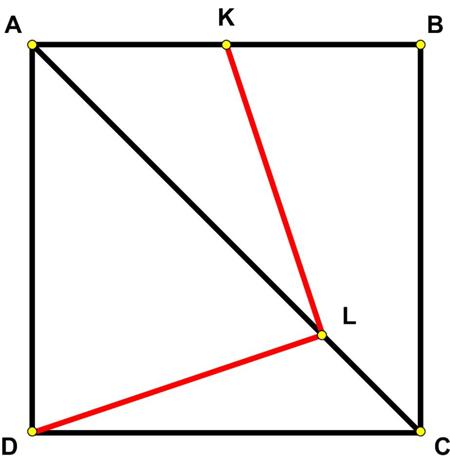 Here is another problem from the “Challenges” section of the Quantum magazine.
Here is another problem from the “Challenges” section of the Quantum magazine.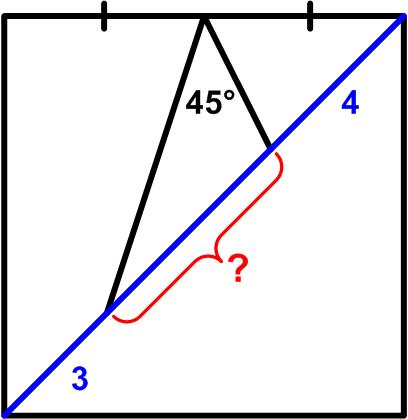 Henk Reuling posted a deceptively simple-looking geometric
Henk Reuling posted a deceptively simple-looking geometric