 I have written about this a bit in my “Symbolic Algebra Timelines” post as part of the discussion of how Greek mathematics got transmitted to the present.
I have written about this a bit in my “Symbolic Algebra Timelines” post as part of the discussion of how Greek mathematics got transmitted to the present.
I had read an article by the renowned literary historian Gilbert Highet some sixty years ago which I never forgot. It discussed in some detail the miracle of the survival of records from the past. I tried to find a copy online, but in vain. So I purchased a used 1962 copy of the now extinct Horizons that contained the article and proceeded to digitize it. Since the subject of the article is about disappearing writings of the past and how some managed to survive through reproduction, I feel it somewhat apropos that I allow it to see the light of day again. He is a marvelous writer and covers the subject with fascinating detail.
Even with all the losses Highet records, writings still survived because they were in some sort of hard copy form. By 1962 fragile documents such as newspapers were being moved to microfilm. But microfilm was often replaced by magnetic tape, which was in turn replaced by a succession of digital media: floppy discs, CDs, DVDs, memory sticks, and so on. Finally, local media is being replaced by files in the “cloud”. All these media are subject to deterioration and loss, or the whims of the custodians. And of course, they all need machines and software to retrieve their information—technology which may no longer exist. Terabytes of moon data are lost on Ampex magnetic tapes for which there are no analog tape readers or even records of the data formats. Even now, some books are being published electronically and not in hard copy. Some people have referred to this ephemeral situation as the “digital Dark Age” where everything can be lost—often in an instant. So perhaps we are lucky that records from the past were not digital.
My copy of Highet’s article appears in two forms: a full, but very large, version with all the color figures, Survival of Records (58 MB), and a text-only smaller version, Survival of Records wo figs (700 KB).
Post Views: 136
 Presh Talwalkar has an interesting new problem.
Presh Talwalkar has an interesting new problem.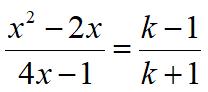 ”
”
 This is a nice problem from Five Hundred Mathematical Challenges.
This is a nice problem from Five Hundred Mathematical Challenges. This is a 2017 Center of Mathematics Problem of the Week.
This is a 2017 Center of Mathematics Problem of the Week. This is an interesting algebra
This is an interesting algebra 

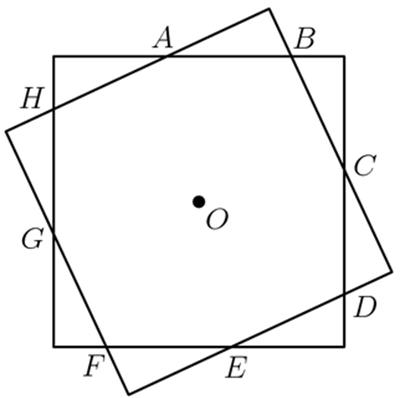 This is a fairly straight-forward problem from the 1999 AIME problems.
This is a fairly straight-forward problem from the 1999 AIME problems. I have written about this a bit in my “Symbolic Algebra Timelines”
I have written about this a bit in my “Symbolic Algebra Timelines”  Presh Talwalkar presented an interesting puzzle that originated in the Ladies’ Diary of 1739-40, was recast by Henry Dudeney in 1917, and further modified using American money.
Presh Talwalkar presented an interesting puzzle that originated in the Ladies’ Diary of 1739-40, was recast by Henry Dudeney in 1917, and further modified using American money. This is a rather mind-boggling problem from the 1947 Eureka magazine.
This is a rather mind-boggling problem from the 1947 Eureka magazine.