 An amazing publication was conceived primarily for women at the beginning of the 18th century in 1704 and was called The Ladies’ Diary or Woman’s Almanack. What made it even more remarkable was that each issue contained mathematical problems whose solutions from the readers were provided in the next issue. One particularly sharp woman was Mary Wright (Mrs. Mary Nelson). This is one of her problems:
An amazing publication was conceived primarily for women at the beginning of the 18th century in 1704 and was called The Ladies’ Diary or Woman’s Almanack. What made it even more remarkable was that each issue contained mathematical problems whose solutions from the readers were provided in the next issue. One particularly sharp woman was Mary Wright (Mrs. Mary Nelson). This is one of her problems:
“VIII. Question 72 by Mrs. Mary Nelson
(proposed in 1719, answered in 1720)
A prize was divided by a captain among his crew in the following manner: the first took 1 pound and one hundredth part of the remainder; the second 2 pounds and one hundredth part of the remainder; the third 3 pounds and one hundredth part of the remainder; and they proceeded in this manner to the last, who took all that was left, and it was then found that the prize had by this means been equally divided amongst the crew. Now if the number of men of which the crew consisted be added to the number of pounds in each share, the square of that sum will be four times the number of pounds in the chest: How many men did the crew consist of, and what was each share?”
What makes this problem nice is that it does have a clean answer, contrary to most of the problems in The Ladies’ Diary.
Answer.
See the Ladies’ Diary Problem for solutions.
(Update 5/6/2019) Continue reading →
 Here is a problem from the UKMT Senior (17-18 year-old) Mathematics Challenge for 2012:
Here is a problem from the UKMT Senior (17-18 year-old) Mathematics Challenge for 2012:
 This is a fun problem from Mathematical Quickies (1967).
This is a fun problem from Mathematical Quickies (1967).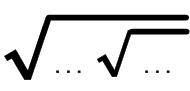 This is another UKMT Senior Challenge problem, but for the year 2005. I thought it was diabolical and hadn’t a clue how to solve it. Even after reading the solution, I don’t think I could have come up with it. I take my hat off to anyone who solves it.
This is another UKMT Senior Challenge problem, but for the year 2005. I thought it was diabolical and hadn’t a clue how to solve it. Even after reading the solution, I don’t think I could have come up with it. I take my hat off to anyone who solves it.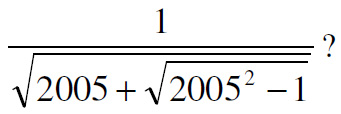
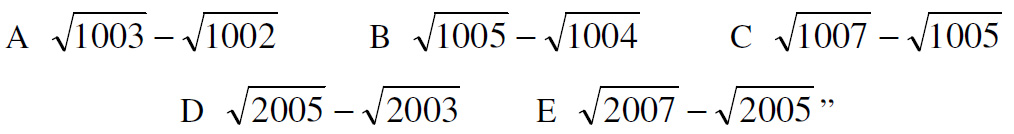
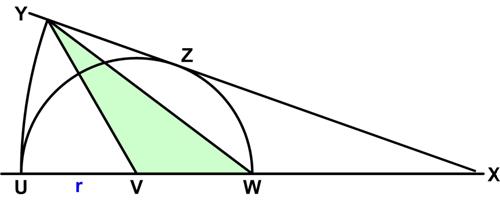
 This is a problem from the UKMT Senior Challenge for 2001. (It has been slightly edited to reflect the colors I added to the diagram.)
This is a problem from the UKMT Senior Challenge for 2001. (It has been slightly edited to reflect the colors I added to the diagram.) Yet another train problem from H. E. Dudeney.
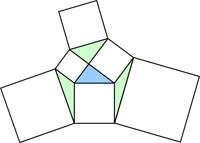
Yet another train problem from H. E. Dudeney.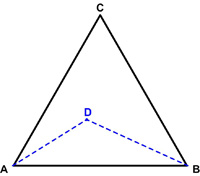 Catriona Shearer retweeted the following problem from Antonio Rinaldi
Catriona Shearer retweeted the following problem from Antonio Rinaldi 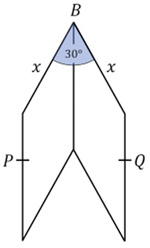 Another challenging problem from
Another challenging problem from  Here is a problem from the UKMT Senior (17-18 year-old) Mathematics Challenge for 2012:
Here is a problem from the UKMT Senior (17-18 year-old) Mathematics Challenge for 2012: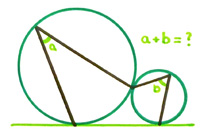 I really was trying to stop including
I really was trying to stop including  An amazing publication was conceived primarily for women at the beginning of the 18th century in 1704 and was called The Ladies’ Diary or Woman’s Almanack. What made it even more remarkable was that each issue contained mathematical problems whose solutions from the readers were provided in the next issue. One particularly sharp woman was Mary Wright (Mrs. Mary Nelson). This is one of her problems:
An amazing publication was conceived primarily for women at the beginning of the 18th century in 1704 and was called The Ladies’ Diary or Woman’s Almanack. What made it even more remarkable was that each issue contained mathematical problems whose solutions from the readers were provided in the next issue. One particularly sharp woman was Mary Wright (Mrs. Mary Nelson). This is one of her problems: