Tag Archives: calculus

Movie Projector Problem

Here is another Brain Bogglers problem from 1987.

“Exactly four minutes after starting to run—when the take-up reel was rotating one and a half times as fast as the projecting reel—the film broke. (The hub diameter of the smaller take-up reel is 8 cm and the hub diameter of the projecting reel is 12 cm.) How many minutes of film remain to be shown?”

This feels like another problem where there is insufficient information to solve it, and that makes it fun and challenging. In fact, I was stumped for a while until I noticed something that was the key to completing the solution.

Answer.

See the Movie Projector Problem for a solution.

Pairwise Products

This 2005 four-star problem from Colin Hughes at Maths Challenge is also a bit challenging.

“Problem
For any set of real numbers, R = {x, y, z}, let sum of pairwise products,
________________S = xy + xz + yz.
Given that x + y + z = 1, prove that S ≤ 1/3.”

Again, I took a different approach from Maths Challenge, whose solution began with an unexplained premise.

See the Pairwise Products

Maximum Product

This 2007 four-star problem from Colin Hughes at Maths Challenge is definitely a bit challenging.

“Problem
For any positive integer, k, let Sk = {x1, x2, … , xn} be the set of [non-negative] real numbers for which x1 + x2 + … + xn = k and P = x1 x2 … xn is maximised. For example, when k = 10, the set {2, 3, 5} would give P = 30 and the set {2.2, 2.4, 2.5, 2.9} would give P = 38.25. In fact, S10 = {2.5, 2.5, 2.5, 2.5}, for which P = 39.0625.

Prove that P is maximised when all the elements of S are equal in value and rational.”

I took a different approach from Maths Challenge, but for me, it did not rely on remembering a somewhat obscure formula. (I don’t remember formulas well at my age—only procedures, processes, or proofs, which is ironic, since at a younger age it was just the opposite.) It is also clear from the Maths Challenge solution that the numbers were assumed to be non-negative.

See Maximum Product.

Infinite Product Problem

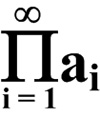This is a challenging problem from Mathematical Quickies (1967).

“Evaluate the infinite product:”

I came up with a motivated solution using some standard techniques from calculus. Mathematical Quickies had a solution that did not employ calculus, but one which I felt used unmotivated tricks.

Answer.

See the Infinite Product Problem for solutions.

Conical Bottle Problem

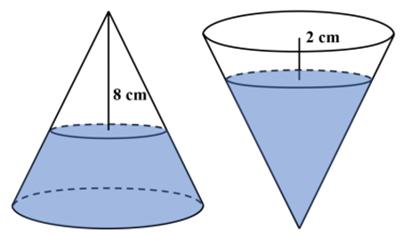I was astonished that this problem was suitable for 8th graders. First of all the formula for the volume of a cone is one of the least-remembered of formulas, and I certainly never remember it. So my only viable approach was calculus, which is probably not a suitable solution for an 8th grader.

Presh Talwalkar: “This was sent to me as a competition problem for 8th graders, so it would be a challenge problem for students aged 12 to 13. When a conical bottle rests on its flat base, the water in the bottle is 8 cm from its vertex. When the same conical bottle is turned upside down, the water level is 2 cm from its base. What is the height of the bottle? (Note “conical” refers to a right circular cone as is common usage.) I at first thought this problem was impossible. But it actually can be solved.”

Answer.

See the Conical Bottle Problem for solutions.

Regiomontanus 1471 Problem

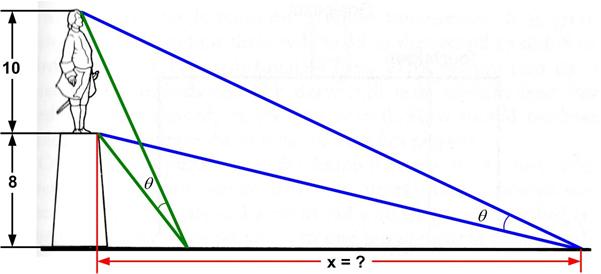This is an old problem I had seen before. Here is David Wells’s rendition:

“Johannes Müller, named Regiomontanus after the Latin translation of Körnigsberg, his city of birth, later made famous by Euler, proposed this problem in 1471. … it is usually put in this form …: From what distance will a statue on a plinth appear largest to the eye [of a mouse!]? If we approach too close, the statue appears foreshortened, but from a distance it is simply small.”

I have added height numbers in feet for concreteness (as well as the mouse qualification, since the angles are measured from ground level). So the problem is to find the distance x such that the angle is maximal.

Answer.

See the Regiomontanus 1471 Problem for solutions.

Straight and Narrow Problem

The following interesting behavior was found at the Futility Closet website:

“A pleasing fact from David Wells’ Archimedes Mathematics Education Newsletter: Draw two parallel lines. Fix a point A on one line and move a second point B along the other line. If an equilateral triangle is constructed with these two points as two of its vertices, then as the second point moves, the third vertex C of the triangle will trace out a straight line. Thanks to reader Matthew Scroggs for the tip and the GIF.”

This is rather amazing and cries out for a proof. It also raises the question of how anyone noticed this behavior in the first place. I proved the result with calculus, but I wonder if there is a slicker way that makes it more obvious. See the Straight and Narrow Problem.

(Update 3/25/2019) Continue reading →

Square Wheels

I came across the following problem from an Italian high school exam on the British Aperiodical website presented by Adam Atkinson:

“There have been various stories in the Italian press and discussion on a Physics teaching mailing list I’m accidentally on about a question in the maths exam for science high schools in Italy last week. The question asks students to confirm that a given formula is the shape of the surface needed for a comfortable ride on a bike with square wheels.

What do people think? Would this be a surprising question at A-level in the UK or in the final year of high school in the US or elsewhere?”

I had seen videos of riding a square-wheeled bicycle over a corrugated surface before, but I had never inquired about the nature of the surface. So I thought it would be a good time to see if I could prove the surface (cross-section) shown would do the job. See Square Wheels.

(Update 9/14/2023)  Square Bridge That Rolls!

This is an incredible application of the rolling square wheels idea described on Matt Parker’s Stand-up Maths Youtube website.  It also demonstrates the difference between engineering and pure math.  The engineers had to solve some challenging problems to adapt the theoretical math to a practical application.  And such solutions are always required under tight time constrictions.  Engineering certainly is a noble profession.

Three Coffin Problems

These are three “Coffin” Problems posed by Nakul Dawra on his Youtube site GoldPlatedGoof. (Nakul is extraordinarily entertaining and mesmerizing.) The origin of the name is explained, but basically they are problems that have easy or even trivial solutions—once you see the solution. But just contemplating the problem, they seem impossible. The idea was to kill the chances of the pupil taking an (oral) exam with these problems. I was able to solve the first two problems (after a while), but I could not figure out the third. See the Three Coffin Problems.

  1. Pages:
  3. 1
  4. 2
  5. 3
  6. 4