Tag Archives: algebra

A Divine Language

I have just finished reading a most remarkable book by Alec Wilkinson, called A Divine Language: Learning Algebra, Geometry, and Calculus at the Edge of Old Age.  I had read an essay of his in the New Yorker that turned out to be essentially excerpts from the book.  I was so impressed with his descriptions of mathematics and intrigued by the premise of a mature adult in his 60s revisiting the nightmare of his high school experience with mathematics that I was eager to see if the book was as good as the essay.  It was, and more.

The book is difficult to categorize—it is not primarily a history of mathematics, as suggested by Amazon. But it is fascinating on several levels.  There is the issue of a mature perspective revisiting a period of one’s youth; the challenges of teaching a novice mathematics, especially a novice who has a strong antagonism for the subject; and insights into why someone would want to learn a subject that can be of no “use” to them in life, especially their later years.

Wilkinson has a strong philosophical urge; he wanted to understand the role of mathematics in human knowledge and the perspective it brought to life.  He was constantly asking the big questions:  is mathematics discovered or invented, what is the balance between nature and nurture, why does mathematics seem to describe the world so well,  what is the link between memorization and understanding, how do you come to understand anything?

See A Divine Language

15 Degree Triangle Puzzle

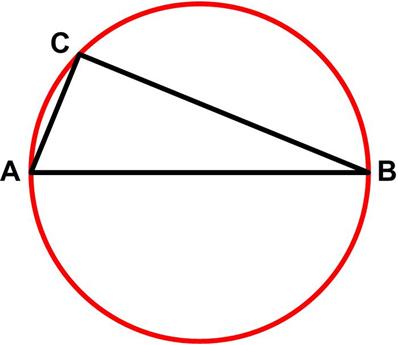This math problem from Colin Hughes’s Maths Challenge website (mathschallenge.net) is a bit more challenging.

“In the diagram, AB represents the diameter, C lies on the circumference of the circle, and you are given that

(Area of Circle) / (Area of Triangle) = 2π.

Prove that the two smaller angles in the triangle are exactly 15° and 75° respectively.”

See the 15 Degree Triangle Puzzle

Two Candles

This is another candle burning problem, presented by Presh Talwalkar.

“Two candles of equal heights but different thicknesses are lit. The first burns off in 8 hours and the second in 10 hours. How long after lighting, in hours, will the first candle be half the height of the second candle? The candles are lit simultaneously and each burns at a constant linear rate.”

Answer.

See Two Candles for solutions.

Hard Time Conundrum

This problem comes from the “Problems Drive” section of the Eureka magazine published in 1955 by the Archimedeans at Cambridge University, England.  (“The problems drive is a competition conducted annually by the Archimedeans. Competitors work in pairs and are allowed five minutes per question ….”)

“There are ten times as many seconds remaining in the hour as there are minutes remaining in the day. There are half as many minutes remaining in the day as there will be hours remaining in the week at the end of the day.  What time is it on what day?”

One of the hardest parts of the problem is just being able to translate the statements into mathematical terms.  Solvable in 5 minutes?!!!

Answer.

See the Hard Time Conundrum for a solution.

Polynomial Division Problem

Here is a challenging problem from the Polish Mathematical Olympiads published in 1960.

“22. Prove that the polynomial

x44 + x33 + x22 + x11 + 1

is divisible by the polynomial

x4 + x3 + x2 + x + 1.”

See the Polynomial Division Problem

(Update 8/23/2021)  The idea expressed in this post that mathematicians are “lazy” and seek short-cuts to solving questions and problems, as I did in this one, was recently the subject of a Numberphile post by Marcus du Sautoy: “Mathematics is all about SHORTCUTS“.

The Pearl Necklace Problem

This problem comes from the Scottish Mathematical Council (SMC) Senior Mathematical Challenge of 2008:

“S2. In Tiffany’s, a world famous jewellery store, there is a string necklace of 33 pearls. The middle one is the largest and most valuable. The pearls are arranged so that starting from one end, each pearl is worth $100 more than the preceding one, up to [and including] the middle one; and starting from the other end, each pearl is worth $150 more than the preceding one, up to [and including] the middle one. If the total value of the necklace is $65,000 what is the value of the largest pearl?”

I included the words in brackets to erase any ambiguity.

Answer.

See the Pearl Necklace Problem for solutions.

Fashion Puzzle

Again we have a puzzle from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos).

“On one occasion, Holmes and I were asked to, solve the robbery of a number of dresses from the workshop of a recently deceased ladies’ tailor to the upper echelons of society. Holmes took a short look at the particulars of the case, and sent them all back to the gown-maker’s son with a scribbled note to the effect that it could only be one particular seamstress, with the help of her husband.

However, glancing through my observations some period later, I observed certain facts about the robbery which led me to an interesting little exercise. The stock at the workshop had been very recently valued at the princely sum of £1,800, and when examined after the theft, comprised of precisely 100 completed dresses in a range of styles, but of equal valuation. However, there was no remaining record of how many dresses had been there beforehand. The son did recall his father stating, of the valuation, that if he’d had thirty. dresses more, then a valuation of £1,800 would have meant £3 less per dress.

Are you able to calculate how many dresses were stolen?”

Answer.

See the Fashion Puzzle for solutions.

Old Hook Puzzle

Here is another, more challenging, problem from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos).

“An event that occurred during The Adventure of the Wandering Bishops inspired Holmes to devise a particularly tricky little mental exercise for my ongoing improvement. There were times when I thoroughly appreciated and enjoyed his efforts, and times when I found them somewhat unwelcome. I’m afraid that this was one of the latter occasions. It had been a bad week.

‘Picture three farmers,’ Holmes told me. ‘Hooklanders. We’ll call them Ern, Ted, and Hob.’

‘If I must,’ I muttered.

‘It will help,’ Holmes replied. ‘Ern has a horse and cart, with an average speed of eight mph. Ted can walk just one mph, given his bad knee, and Hob is a little better at two mph, thanks to his back.’

‘A fine shower,’ I said. ‘Can’t I imagine them somewhat fitter?’

‘Together, these worthies want to go from Old Hook to Coreham, a journey of 40 miles. So Ern got Ted in his cart, drove him most of the way, and dropped him off to walk the rest. Then he went back to get Hob [who was still walking], and took him into Coreham, arriving exactly as Ted did. How long did the journey take?’

Can you find a solution?”

I added the statement in brackets.  I initially thought Hob waited in Old Hook until Ted fetched him.  But the solution indicated that was not the case.  So I realized Hob had started out at the same time as the others. The solution has some hairy arithmetic.  Even knowing the answer it is difficult to do the computations without a mistake.

Answer.

See the Old Hook Puzzle for solutions.

  1. Pages:
  3. 1
  4. 2
  5. 3
  6. 4
  7. 5
  8. 6