This is a tricky product problem from Alfred Posamentier which naturally has a slick solution—if you can think of it.
“Find the numerical value of the following expression:
“_
See A Tricky Product for a solution.
Tag Archives: algebra
Radical Radicals
This is another UKMT Senior Challenge problem, but for the year 2005. I thought it was diabolical and hadn’t a clue how to solve it. Even after reading the solution, I don’t think I could have come up with it. I take my hat off to anyone who solves it.
“Which of the following is equal to
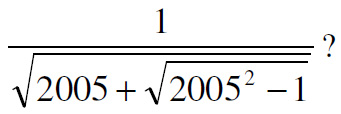
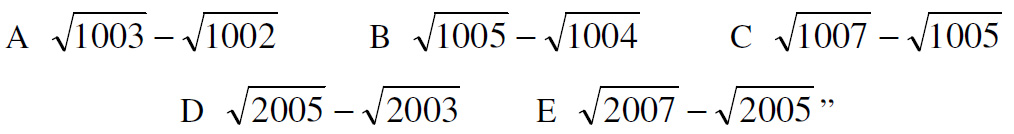
See Radical Radicals for a solution.
Challenging Sum
Here is a problem from the UKMT Senior (17-18 year-old) Mathematics Challenge for 2009:
“Four positive integers a, b, c, and d are such that
abcd + abc + bcd + cda + dab + ab + bc + cd + da + ac + bd + a + b + c + d = 2009.
What is the value of a + b + c + d?
A 73_________B 75_________C 77_________D 79_________E 81”
See the Challenging Sum for a solution.
(Update 4/17/2019) Continue reading