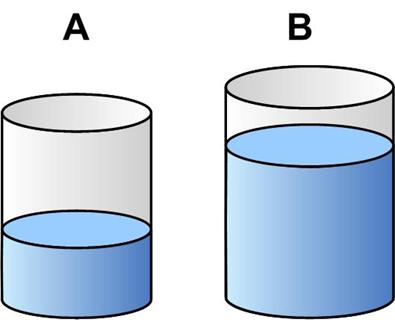
 This is a slightly different type of a mixture problem from Dan Griller.
This is a slightly different type of a mixture problem from Dan Griller.
“Two containers A and B sit on a table, partially filled with water. First, 40% of the water in A is poured into B, which completely fills it. Then 75% of the water in B is poured into A, which completely fills it. 80% of the water in A is poured into B, which completely fills it. Calculate the ratio of the capacity of container A to the capacity of container B, and the fraction of container A that was occupied by water at the start.”
See the Two Containers Mixing Puzzle for solution.

 This is another race puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings for 2013.
This is another race puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings for 2013.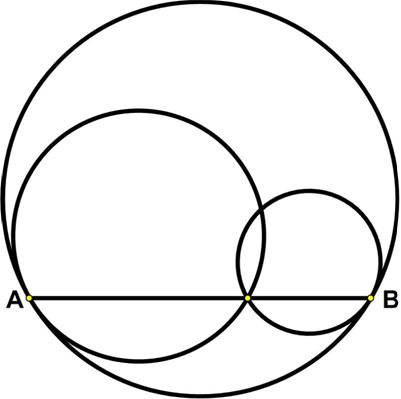 Here is another problem from the “Challenges” section of the Quantum magazine.
Here is another problem from the “Challenges” section of the Quantum magazine.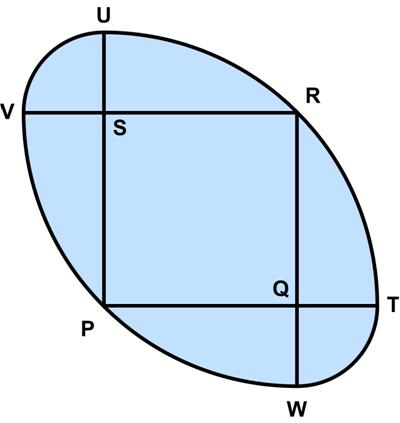 Here is another UKMT Senior Challenge problem for 2017.
Here is another UKMT Senior Challenge problem for 2017.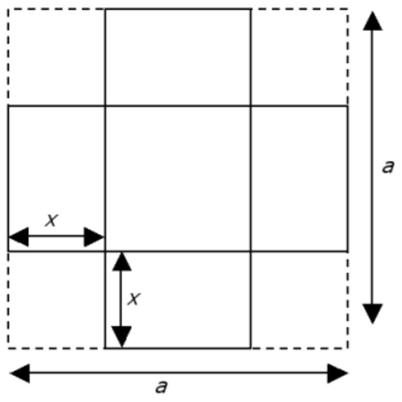 This problem is from Colin Hughes’s Maths Challenge website (mathschallenge.net).
This problem is from Colin Hughes’s Maths Challenge website (mathschallenge.net). Here is another classic example of the three jug problem posed in the Mathigon Puzzle Calendars for 2017.
Here is another classic example of the three jug problem posed in the Mathigon Puzzle Calendars for 2017. This is a most surprising and amazing identity from the 1965 Polish Mathematical Olympiads.
This is a most surprising and amazing identity from the 1965 Polish Mathematical Olympiads.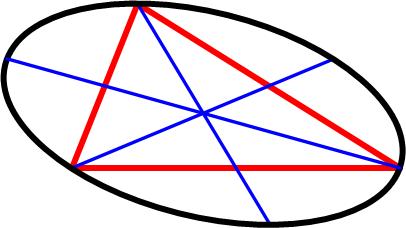 This is a tantalizing problem from the 1977 Crux Mathematicorum.
This is a tantalizing problem from the 1977 Crux Mathematicorum. This is a somewhat challenging problem from the 1997 American Invitational Mathematics Exam (AIME).
This is a somewhat challenging problem from the 1997 American Invitational Mathematics Exam (AIME). This is a nifty
This is a nifty