 Here is another simply amazing problem from Five Hundred Mathematical Challenges:
Here is another simply amazing problem from Five Hundred Mathematical Challenges:
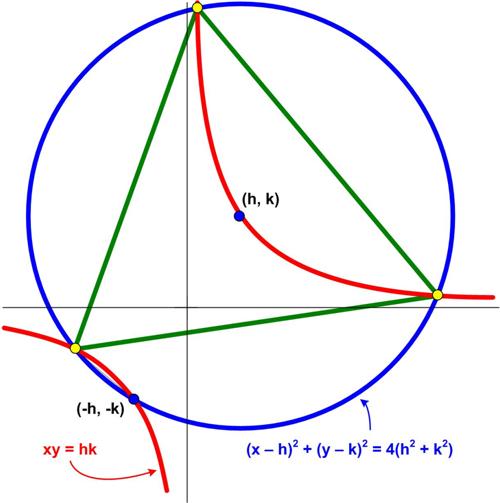
“Problem 154. Show that three solutions, (x1,.y1), (x2,.y2), (x3, y3), of the four solutions of the simultaneous equations
____________(x – h)² + (y – k)² = 4(h² + k²)
______________________xy = hk
are vertices of an equilateral triangle. Give a geometrical interpretation.”
Again, I don’t see how anyone could have discovered this property involving a circle, a hyperbola, and an equilateral triangle. It seems plausible when h.=.k, but it is not at all obvious for h.≠.k. For some reason, I had difficulty getting a start on a solution, until the obvious approach dawned on me. I don’t know why it took me so long.
See the Amazing Triangle Problem.

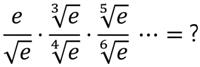 This is a delightful and surprising problem from
This is a delightful and surprising problem from  Here is another train puzzle, this time from J. A. H. Hunter’s Entertaining Mathematical Teasers:
Here is another train puzzle, this time from J. A. H. Hunter’s Entertaining Mathematical Teasers: It is hard to believe a whole year has passed since I started this blog. What is even more surprising is that by February I thought I was about done. I had more or less uploaded the math curiosities and problems I had been thinking about over the years and had presented most of the math essays I had written. There are of course only a finite number of math problems in the world, so I thought I was about done. But much to my surprise I kept finding one more thing that interested me, either an essay or math problem. So here I am. We will have to see what the next year brings.
It is hard to believe a whole year has passed since I started this blog. What is even more surprising is that by February I thought I was about done. I had more or less uploaded the math curiosities and problems I had been thinking about over the years and had presented most of the math essays I had written. There are of course only a finite number of math problems in the world, so I thought I was about done. But much to my surprise I kept finding one more thing that interested me, either an essay or math problem. So here I am. We will have to see what the next year brings.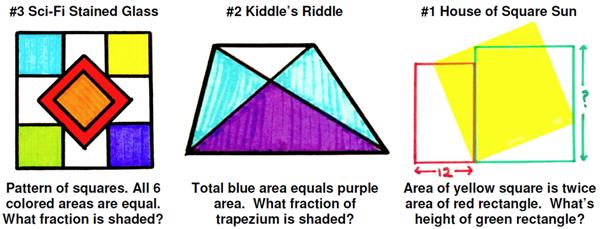 I have been subverted again by a recent post by Ben Orlin, “
I have been subverted again by a recent post by Ben Orlin, “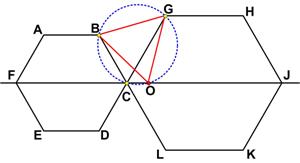 This is truly an amazing result from Five Hundred Mathematical Challenges.
This is truly an amazing result from Five Hundred Mathematical Challenges.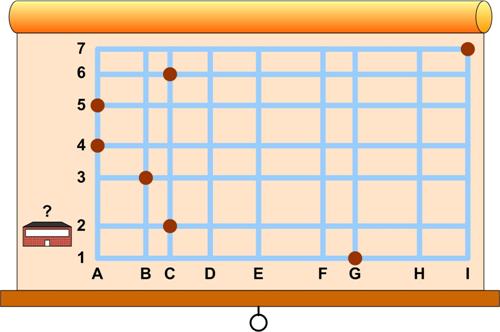 This is a somewhat elegant problem from the 1987 Discover magazine’s Brain Bogglers by Michael Stueben:
This is a somewhat elegant problem from the 1987 Discover magazine’s Brain Bogglers by Michael Stueben: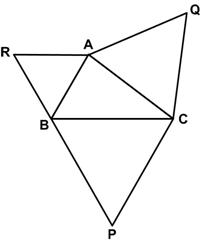 Here is another simple problem from Futility Closet.
Here is another simple problem from Futility Closet. If you will pardon the pun, this is a diabolical problem from the collection Five Hundred Mathematical Challenges.
If you will pardon the pun, this is a diabolical problem from the collection Five Hundred Mathematical Challenges. Here is another Brain Bogglers problem from 1987.
Here is another Brain Bogglers problem from 1987.