 Twitter comments to the recently released GDP growth numbers for the Third Quarter reminded me of an old trap regarding percentages. The financial and technical articles were accurate, but the comments by Twitter users often reflected the pitfall.
Twitter comments to the recently released GDP growth numbers for the Third Quarter reminded me of an old trap regarding percentages. The financial and technical articles were accurate, but the comments by Twitter users often reflected the pitfall.
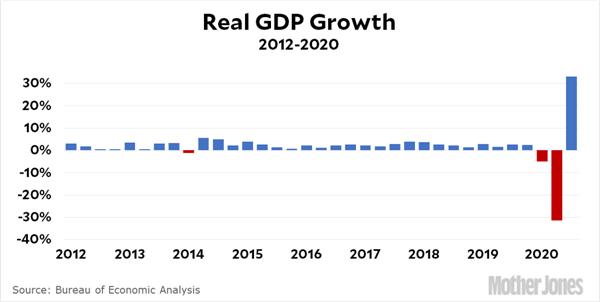
After a Second Quarter annualized US GDP fall of about 33%, the Third Quarter showed a gain of about 33%. So some commenters thought the gain canceled the previous loss.
But of course a Q2 loss of 33% or 1/3, means the GDP is 2/3 of what it was. So a 33% or 1/3 gain means the new level will be 4/3 of the previous 2/3 level or 8/9 ≈ 90% of the original level. So the gain does not cancel the loss. Kevin Drum’s subsequent diagram makes that clear:
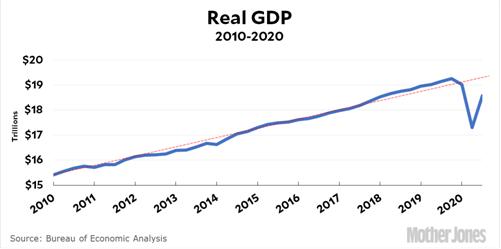
To make the situation even clearer, suppose there were a 90% loss in Q2 leaving 10% of the original GDP. Then a 90% gain in Q3 would be 1.9 x 0.1 = .19 or 19% of the original GDP, reflecting a net loss of 81% for the two quarters.
(Update 11/5/2020) Actually, this probably can be seen more clearly as follows. Let x be the fraction of change in the two quarters. That is, x is the fraction of loss in the first quarter and then x is also the fraction of gain in the second. Therefore, the total change over the two quarters will be (1 + x)(1 – x) = 1 – x2. In our first example x = 1/3, so the resulting change was 1 – 1/9 = 8/9 ≈ 0.9. In the second example, x = .9, so the resulting change was 1 – .81 = .19. Clearly, these changes will never restore the original amount.
