Recently I viewed a startling video by Matt Parker about the Tupper Self-Referential Formula. It is a formula that visually represents itself when graphed at a specific location in the (x, y) plane. I found it difficult to fathom, so I looked it up on Wikipedia and Google. After reading different explanations, I finally think I have the idea. So thought I would add my version to the mix. See Tupper Self-Referential Formula.
Category Archives: Curiosities and Questions
Corner Reflectors
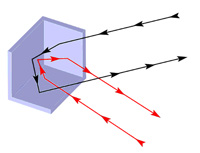I came across the following entry in the Futility Closet website that cried out for justification. “An arrangement of three mutually perpendicular planes, like those in the corner of a cube, have a pleasing property: They’ll reflect a ray of light back in the direction that it came from.” So the question is, why is this reflection property true? See Corner Reflectors.
The Pythagorean Theorem
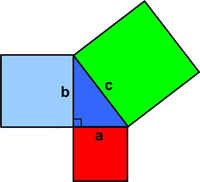All too frequently I come across the usual statements questioning why non-technical folks should bother studying math. A typical example is the Pythagorean Theorem. People say, “What good is that? I’ll never use it. So why bother?” Ah, the famous “utility” argument – as if everything worthwhile must be “useful.” I thought I would take this “useless” math example par excellence and show that, in fact, it harbors many of the best aspects of mathematics that anyone should find appealing. See the Pythagorean Theorem
Slow Lane Problem
Paul Krugman in his 26 July 2013 New York Times column “The Conscience of a Liberal” provided an analysis about why we are always being caught in the slow lane of a congested highway. I tried to fill in the gaps in his laconic explanation. See the Slow Lane Problem.
Three Jugs Problem
Years ago (1967) I read about an interesting solution to the three jugs problem in a book by Nathan Court which involved the idea of a billiard ball traversing a skew billiard table with distributions of the water between the jugs listed along the edges of the table. The ball bounced between solutions until it ended on the desired value. I thought it was very clever, but I really did not understand why it worked. Later I figured out an explanation, which I present here. See the Three Jugs Problem.
Earth as Magnet
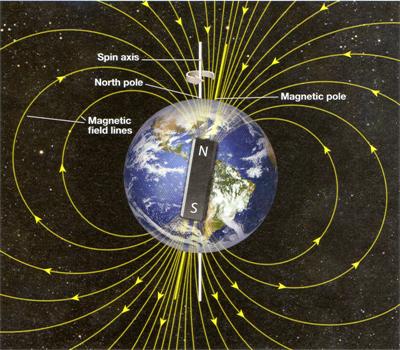This was one of my more satisfying essays. Several years ago I gave some thought to what it meant for the earth to be considered a magnet. More recently in 2012 an article in the magazine BirdWatching brought it all back when I saw its diagram of the earth as a magnet for guiding migratory birds. Knowing that magnets have north and south poles, where should we expect to find the earth’s north and south magnetic poles? See Earth as Magnet.
Vitruvian Man Problem
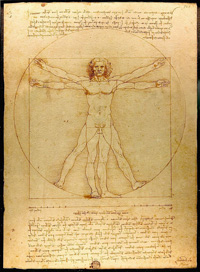This is a mildly pointless 2015 article about Leonardo Da Vinci’s famous drawing of the Vitruvian Man spread-eagled and inscribed in a circle and a square. I started wondering about the positions and whether they over-determined the circle and square. What hidden constraints were being assumed? One assumption turned out to be famous, namely, that the height of a man equaled the distance between his finger tips when he holds his arms straight out to either side of his body. I had been told this in childhood, and I never knew where it came from. Also, I don’t think it is true in every case (what about women?), though it does appear to be close (and is true in my case). See the Vitruvian Man Problem.
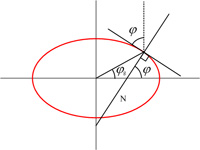
Degree of Latitude
South Dakota Travel Problem
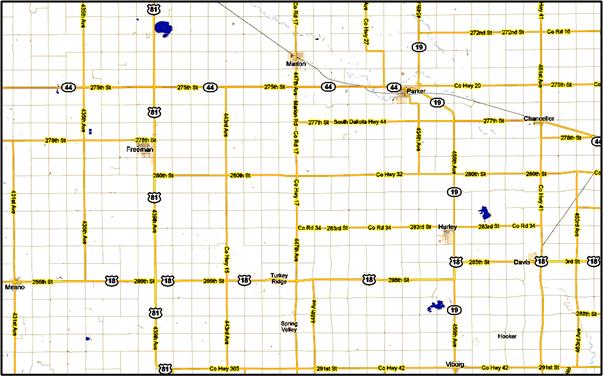This light-weight problem arose from a newspaper article that had me looking at a Google map of the area near Sioux Falls, South Dakota. What I saw was an excellent example of the Taxicab Geometry, allegedly first considered by Hermann Minkowski, mathematical friend of Albert Einstein. The map configuration was perpetrated by the great Public Land Survey System (PLSS) that originated with Thomas Jefferson and spread from Ohio (more or less) west to the California coast. This scheme overlaid the country basically with a 1 mile x 1 mile square grid of roads, and South Dakota is a prime example.
I first confronted the PLSS doing genealogy research, where the grid became a main method for locating the farms of ancestors. I had no idea it was so extensive. A fabulous book about the system and the history of land surveying in America is Andro Linklater’s Measuring America: How the United States Was Shaped By the Greatest Land Sale in History (2002). I learned all about perches and 17th century English mathematician Edmund Gunter’s survey chain, which became an essential tool for so vast a survey undertaking. Regarding the implications of the PLSS in South Dakota, see the South Dakota Travel Problem.
Ancestors Problem
In 2011 I wrote about an amusing article in the 9 September 1978 Washington Post in which the reporter, Henry Allen, began thinking about the number of ancestors he had 10 generations ago. He figured that each generation had 2 parents, so the 10th generation would have 2^10 or over a thousand members. At 25 years per generation he started imagining the expanding number of direct ancestors he had going back through history, achieving astronomical numbers, which did not seem reasonable. As reporters do, he started interviewing people to get to the bottom of the problem. See the Ancestors Problem.
One thing that did come out of the exercise is that I began researching the idea of Most Recent Common Ancestor (MRCA). It led to a number of approaches from statistical to molecular evolution markers. I was hoping to write more about it when I had the time. An example of the statistical approach is the article by Joseph Lachance, “Inbreeding, Pedigree Size, and the Most Recent Common Ancestor of Humanity,” J Theor Biol. 2009 November 21; 261(2): 238–247. Online 2009 August 11. doi: 10.1016/j.jtbi.2009.08.006
(Update 5/10/2019) Continue reading