Tag Archives: trigonometry

The Tired Messenger Problem

Here is another challenging problem from the Polish Mathematical Olympiads. Its generality will cause more thought than for a simpler, specific problem.

“A cyclist sets off from point O and rides with constant velocity v along a rectilinear highway. A messenger, who is at a distance a from point O and at a distance b from the highway, wants to deliver a letter to the cyclist. What is the minimum velocity with which the messenger should run in order to attain his objective?”

See the Tired Messenger Problem

(Update 1/29/2025) Dan Steinitz Solution

Dan Steinitz from Israel has sent an elegant solution that only involves vectors and geometry without calculus. I have edited slightly his email and added excerpts from his whiteboard solution, though without the Hebrew annotations, which unfortunately I cannot read. But that is the glory of the universal language of mathematics: it can be read and understood in any language.

See Dan Steinitz Solution.

Neuberg’s Theorem

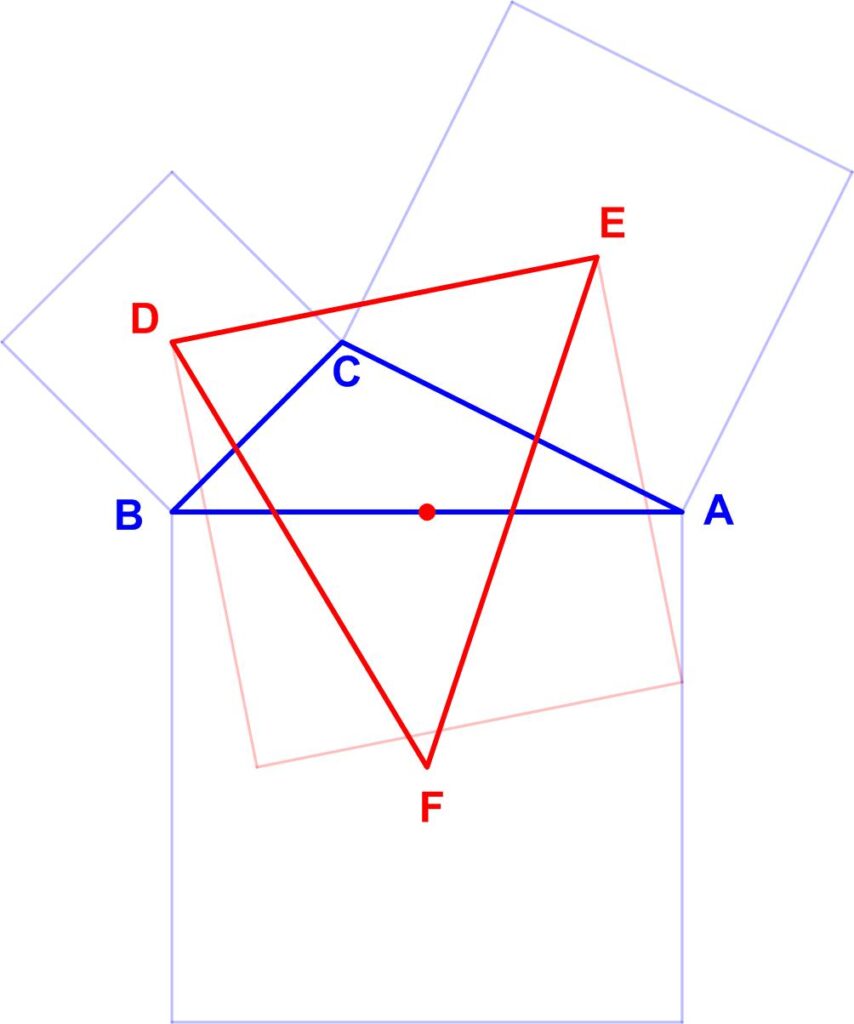This turned out to be a challenging puzzle from the 1980 Canadian Math Society’s magazine, Crux Mathematicorum.

“Proposed by Leon Bankoff, Los Angeles, California.

Professor Euclide Paracelso Bombasto Umbugio has once again retired to his tour d’ivoire where he is now delving into the supersophisticated intricacies of the works of Grassmann, as elucidated by Forder’s Calculus of Extension. His goal is to prove Neuberg’s Theorem:

If D, E, F are the centers of squares described externally on the sides of a triangle ABC, then the midpoints of these sides are the centers of squares described internally on the sides of triangle DEF. [The accompanying diagram shows only one internally described square.]

Help the dedicated professor emerge from his self-imposed confinement and enjoy the thrill of hyperventilation by showing how to solve his problem using only highschool, synthetic, Euclidean, ‘plain’ geometry.”

Alas, my plane geometry capability was inadequate to solve the puzzle that way, so I had to resort to the sledge hammer of analytic geometry, trigonometry, and complex variables.

See Neuberg’s Theorem

15 Degree Triangle Puzzle

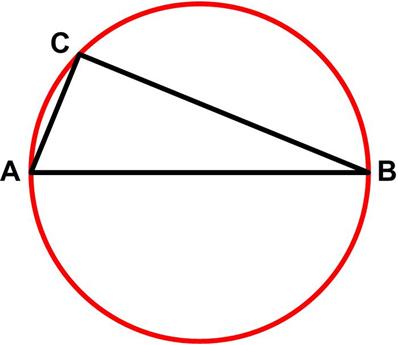This math problem from Colin Hughes’s Maths Challenge website (mathschallenge.net) is a bit more challenging.

“In the diagram, AB represents the diameter, C lies on the circumference of the circle, and you are given that

(Area of Circle) / (Area of Triangle) = 2π.

Prove that the two smaller angles in the triangle are exactly 15° and 75° respectively.”

See the 15 Degree Triangle Puzzle

Topple Blocks Puzzle

This is another imaginative puzzle from MEI’s MathsMonday. I didn’t know what topple blocks were at first, but a previous MathsMonday puzzle defined them as shown in the first frame. Apparently they derive from the game of Jenga created by Leslie Scott and launched in 1983.

See the Topple Blocks Puzzle

Diabolical Triangle Puzzle

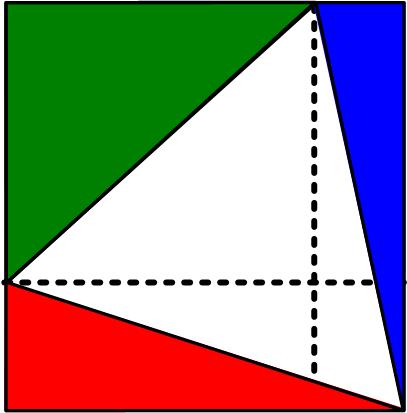This simple-appearing problem is from the 17 August 2020 MathsMonday offering by MEI, an independent curriculum development body for mathematics education in the UK.

“The diagram shows an equilateral triangle in a rectangle. The two shapes share a corner and the other corners of the triangle lie on the edges of the rectangle. Prove that the area of the green triangle is equal to the sum of the areas of the blue and red triangles. What is the most elegant proof of this fact?”

Since the MEI twitter page seemed to be aimed at the high school level and the parting challenge seemed to indicate that there was one of those simple, revealing solutions to the problem, I spent several days trying to find one. I went down a number of rabbit holes and kept arriving at circular reasoning results that assumed what I wanted to prove. Visio revealed a number of fascinating relationships, but they all assumed the result and did not provide a proof. I finally found an approach that I thought was at least semi-elegant.

See the Diabolical Triangle Puzzle

(Update 1/30/2021) New MEI Solution

Lopsided Hexagon Problem

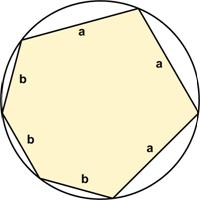Here is another good problem from Five Hundred Mathematical Challenges:

“Problem 100. A hexagon inscribed in a circle has three consecutive sides of length a and three consecutive sides of length b. Determine the radius of the circle.”

This problem made me think of the Putnam Octagon Problem. Again my approach might be considered a bit pedestrian. 500 Math Challenges had a slightly slicker solution.

Answer.

See the Lop-sided Hexagon Problem for solutions.

Hard Geometric Problem

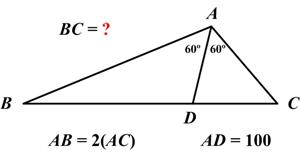This is another problem from the indefatigable Presh Talwalkar.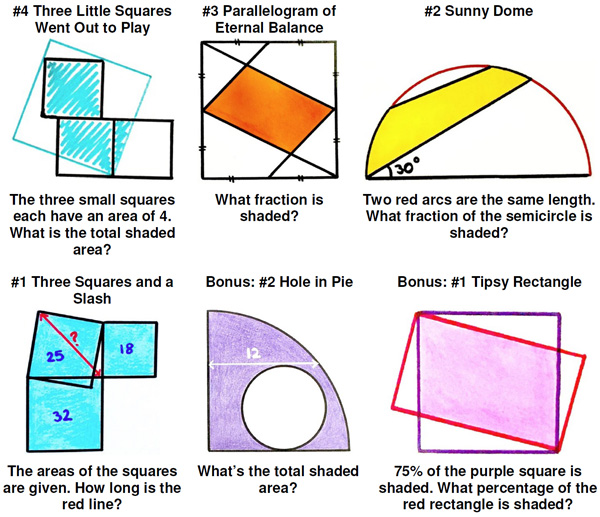

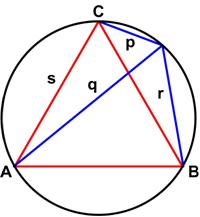_ _____Hard Geometry Problem
“In triangle ABC above, angle A is bisected into two 60° angles. If AD = 100, and AB = 2(AC), what is the length of BC?”

Answer.

See Hard Geometric Problem for solutions.

(Update 7/18/2020, 7/20/2020) Alternative Solution Continue reading →

Geometric Puzzle Munificence

Having fallen under the spell of Catriona Shearer’s geometric puzzles again, I thought I would present the latest group assembled by Ben Orlin, which he dubs “Felt Tip Geometry”, along with a bonus of two more recent ones that caught my fancy as being fine examples of Shearer’s laconic style. Orlin added his own names to the four he assembled and I added names to my two, again ordered from easier to harder.

See Geometric Puzzle Munificence.

(Update 4/16/2020) Ben Orlin has another set of Catriona Shearer puzzles 11 Geometry Puzzles That Drive Mathematicians to Madness which I will leave you to see and enjoy. But I wanted to emphasize some observations he included that I think are spot on. Continue reading →

A Tidy Theorem

This is another fairly simple puzzle from Futility Closet.

“If an equilateral triangle is inscribed in a circle, then the distance from any point on the circle to the triangle’s farthest vertex is equal to the sum of its distances to the two nearer vertices (q = p + r).

(A corollary of Ptolemy’s theorem.)”

See A Tidy Theorem

Geometric Puzzle Madness

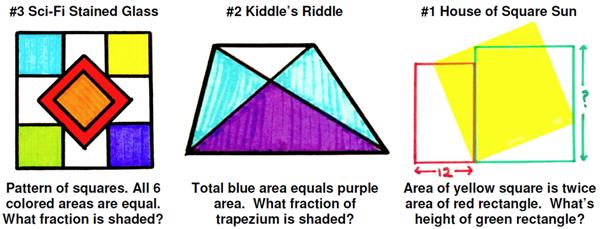I have been subverted again by a recent post by Ben Orlin, “Geometry Puzzles for a Winter’s Day,” which is another collection of Catriona Shearer’s geometric puzzles, this time her favorites for the month of November 2019 (which Orlin seems to have named himself). I often visit Orlin’s blog, “Math with Bad Drawings”, so it is hard to kick my addiction to Shearer’s puzzles if he keeps presenting collections. Her production volume is amazing, especially as she is able to maintain the quality that makes her problems so special.

The Stained Glass puzzle generated some discussion about needed constraints to ensure a solution. Essentially, it was agreed to make explicit that the drawing had vertical and horizontal symmetry in the shapes, that is, flipping it horizontally or vertically kept the same shapes, though some of the colors might be swapped.

See Geometric Puzzle Madness

Meditations on Mathematics

A compendium of puzzles, problems, math inquiries, and math commentary.