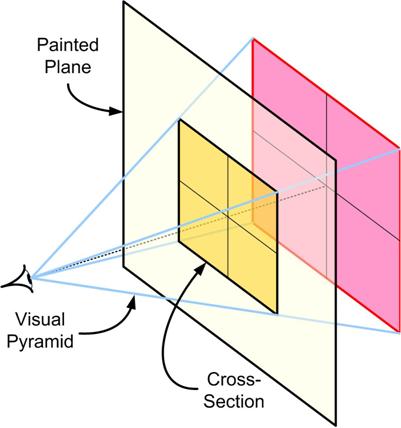I was reading yet another book on the Scientific Revolution when I came across a discussion of the mathematical significance of the invention of perspective for painting in the 15th century Italian Renaissance. The main player in the saga was Leon Battista Alberti (1404 – 1472) and his tome De Pictura (On Painting) (1435-6), which contained the first mathematical presentation of perspective. Even though mathematics was advertised, it was not at the level of trigonometry I used in my post “The Perspective Map”, but rather entailed simple Euclidean plane geometry. So the discussion was largely historical rather than mathematical. Nevertheless, I became curious to learn how much Alberti was able to discover about perspective without a lot of math. This essay is the result.
See Alberti’s Perspective Construction
(Update 7/29/2019) I got a response! Continue reading
An amazing publication was conceived primarily for women at the beginning of the 18th century in 1704 and was called The Ladies’ Diary or Woman’s Almanack. What made it even more remarkable was that each issue contained mathematical problems whose solutions from the readers were provided in the next issue. One particularly sharp woman was Mary Wright (Mrs. Mary Nelson). This is one of her problems:
It is a bit presumptuous to think I could reduce the universe of mathematics to some succinct essence, but ever since I first saw a column in Martin Gardner’s Scientific American Mathematical Games in 1967, I thought his example illustrated the essential feature of mathematics, or at least one of its principal attributes. And he posed it in a way that would be accessible to anyone. I especially wanted to credit Martin Gardner, since the idea resurfaced recently, uncredited, in some attractive videos by Katie Steckles and James Grime. (This reminds me of the Borges idea that “eighty years of oblivion are perhaps equal to novelty”.) See the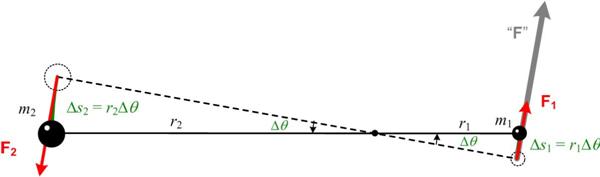 
I have always had a tenuous relationship with the concept of angular momentum, but recently my concerns resurfaced when I did my studies on Kepler, and in particular his 
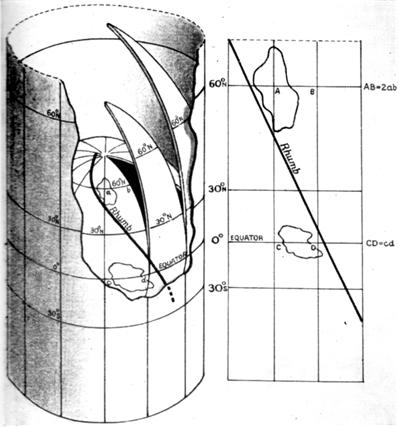Years ago during one of my many excursions into the history of mathematics I wondered how Mercator used logarithms in his map projection (introduced in a 1569 map) when logarithms were not discovered by John Napier (1550-1617) and published in his book Mirifici Logarithmorum Canonis Descriptio until 1614, three years before his death in 1617. The mystery was solved when I read a 1958 book by D. W. Waters which said Edward Wright (1561-1615) in his 1599 book Certaine Errors in Navigation produced his “most important correction, his chart projection, now known as Mercator’s.” Wright did not use logarithms explicitly but rather implicitly through the summing of discrete secants of the latitude as scale factors. But what really caught my attention in the Waters book was this arresting footnote: “Wright explained his projection in terms of a bladder blown up inside a cylinder, a very good analogy.” This article recounts my exploration of this idea. See 
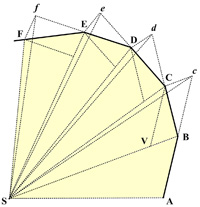I have long been fascinated by Newton’s proof of Kepler’s Equal Areas Law and wanted to write about it. Of course, others have as well, but I wanted to emphasize an aspect of the proof that supported my philosophy of mathematics.
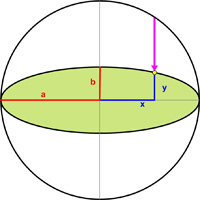I had been exploring how Kepler originally discovered his first two laws and became fascinated by what he did in his Astronomia Nova (1609), as presented by a number of researchers. Among the writers was A. E. L. Davis. She mentioned that the characterization of the ellipse that Kepler was using was the idea of a “compressed circle,” that is, a circle all of whose points were shrunk vertically by a constant amount towards a fixed diameter of the circle. I did not recall ever hearing this idea before and tried to track down its origin together with a proof — futilely, Davis’s references notwithstanding. I then tried to prove it myself. It was easy to do with analytic geometry. But in the spirit of the Kepler era (before the advent of Fermat’s and Descartes’s beginnings at fusing algebra and geometry) I tried to prove it solely within Euclid’s plane geometry. Some critical steps seemed to come from the great work of Apollonius of Perga (262-190 BC) on Conics. But for me a final elegant proof was not evident until 1822 when Dandelin employed his inscribed spheres. See 
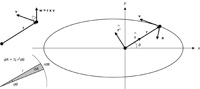Years ago (1963) I got the paperback The Calculus:A Genetic Approach, by Otto Toeplitz, which presented the basic ideas of the differential and integral calculus from a historical point of view. One thing Toeplitz did at the end of his book that I had not seen in other texts was to show the equivalence of Kepler’s Laws and Newton’s Law of Gravity. (Since 1963 David Bressoud has developed this theme in his excellent 1991 text.) I thought I would try to emulate Toeplitz’s approach with more modern notation (vectors) and arguments in hopes of extracting the essential ideas from the clutter.
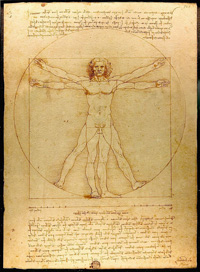This is a mildly pointless 2015 article about Leonardo Da Vinci’s famous drawing of the Vitruvian Man spread-eagled and inscribed in a circle and a square. I started wondering about the positions and whether they over-determined the circle and square. What hidden constraints were being assumed? One assumption turned out to be famous, namely, that the height of a man equaled the distance between his finger tips when he holds his arms straight out to either side of his body. I had been told this in childhood, and I never knew where it came from. Also, I don’t think it is true in every case (what about women?), though it does appear to be close (and is true in my case). See the 
