 Here is another simply amazing problem from Five Hundred Mathematical Challenges:
Here is another simply amazing problem from Five Hundred Mathematical Challenges:
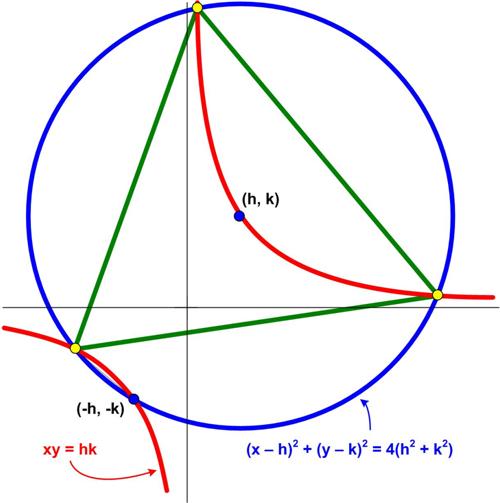
“Problem 154. Show that three solutions, (x1,.y1), (x2,.y2), (x3, y3), of the four solutions of the simultaneous equations
____________(x – h)² + (y – k)² = 4(h² + k²)
______________________xy = hk
are vertices of an equilateral triangle. Give a geometrical interpretation.”
Again, I don’t see how anyone could have discovered this property involving a circle, a hyperbola, and an equilateral triangle. It seems plausible when h.=.k, but it is not at all obvious for h.≠.k. For some reason, I had difficulty getting a start on a solution, until the obvious approach dawned on me. I don’t know why it took me so long.
See the Amazing Triangle Problem.
 This is a nice problem from Five Hundred Mathematical Challenges.
This is a nice problem from Five Hundred Mathematical Challenges.
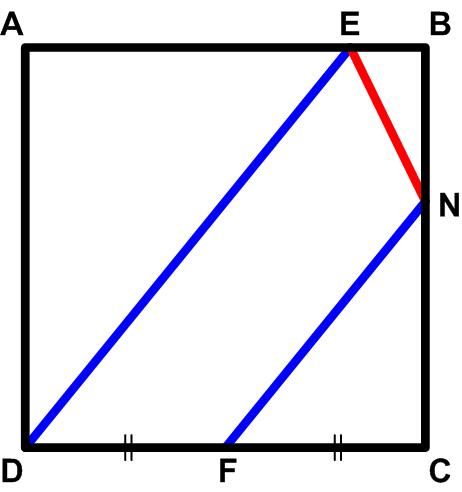 This is an interesting problem from the collection Five Hundred Mathematical Challenges.
This is an interesting problem from the collection Five Hundred Mathematical Challenges. This is a straight-forward problem from Five Hundred Mathematical Challenges.
This is a straight-forward problem from Five Hundred Mathematical Challenges.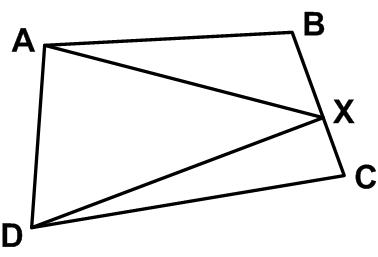 This is another simple problem from Five Hundred Mathematical Challenges:
This is another simple problem from Five Hundred Mathematical Challenges: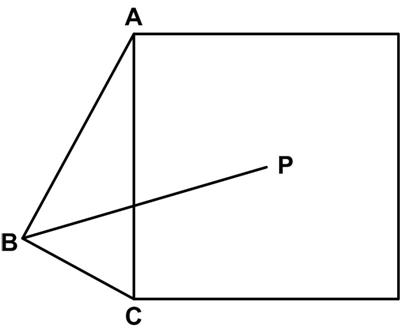 This is a simple problem from Five Hundred Mathematical Challenges:
This is a simple problem from Five Hundred Mathematical Challenges: Here is a fairly straight-forward problem from 500 Mathematical Challenges.
Here is a fairly straight-forward problem from 500 Mathematical Challenges. Here is a problem from Five Hundred Mathematical Challenges that I indeed found quite challenging.
Here is a problem from Five Hundred Mathematical Challenges that I indeed found quite challenging.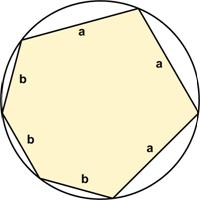 Here is another good problem from Five Hundred Mathematical Challenges:
Here is another good problem from Five Hundred Mathematical Challenges: The following problem from Five Hundred Mathematical Challenges was a challenge indeed, even though it appeared to be a standard travel puzzle.
The following problem from Five Hundred Mathematical Challenges was a challenge indeed, even though it appeared to be a standard travel puzzle. Here is another simply amazing problem from Five Hundred Mathematical Challenges:
Here is another simply amazing problem from Five Hundred Mathematical Challenges: