 This is an intriguing puzzle from Futility Closet.
This is an intriguing puzzle from Futility Closet.
“In Robert Chambers’ 1906 novel The Tracer of Lost Persons, Mr. Keen copies the figure below from a mysterious photograph. He is trying to help Captain Harren find a young woman with whom he has become obsessed.
‘It’s the strangest cipher I ever encountered,’ he says at length. ‘The strangest I ever heard of. I have seen hundreds of ciphers—hundreds—secret codes of the State Department, secret military codes, elaborate Oriental ciphers, symbols used in commercial transactions, symbols used by criminals and every species of malefactor. And every one of them can be solved with time and patience and a little knowledge of the subject. But this … this is too simple.’
The message reveals the name of the young woman whom Captain Harren has been seeking. What is it?”
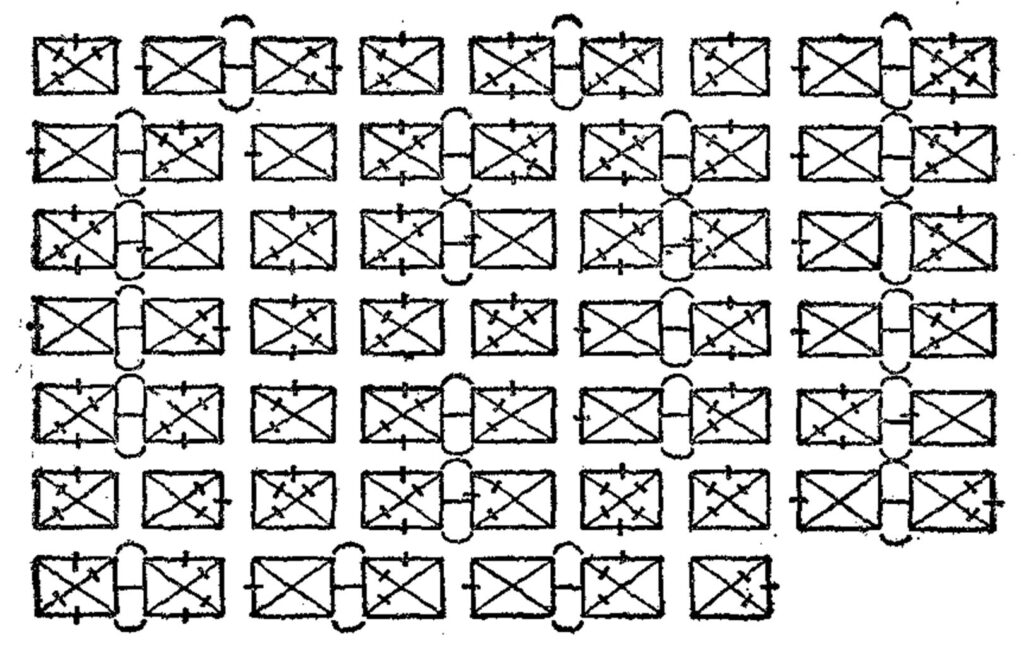
As is usual with these types of puzzles, I felt foolish that I couldn’t see the immediate, simple interpretation of the boxes—after a great deal of effort. So I solved it using the usual cryptographic methods that rely heavily on logic and letter frequencies, though the message is a bit short for that.
See Box Code Puzzle for solutions.

 The following is another puzzle from the Irishman Owen O’Shea.
The following is another puzzle from the Irishman Owen O’Shea. This is a straight-forward problem from Geoffrey Mott-Smith in 1954.
This is a straight-forward problem from Geoffrey Mott-Smith in 1954. This is a relatively simple probability
This is a relatively simple probability  This is a recent Alex Bellos
This is a recent Alex Bellos  This is yet another simple problem from Henry Dudeney.
This is yet another simple problem from Henry Dudeney.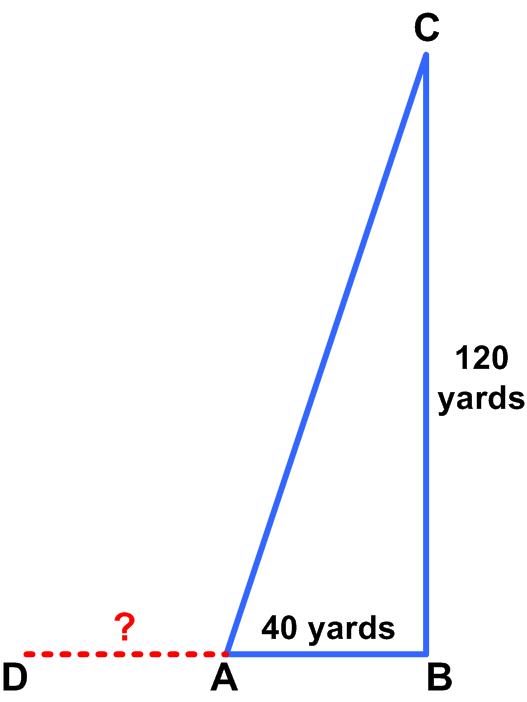 The following puzzle is from the Irishman Owen O’Shea.
The following puzzle is from the Irishman Owen O’Shea.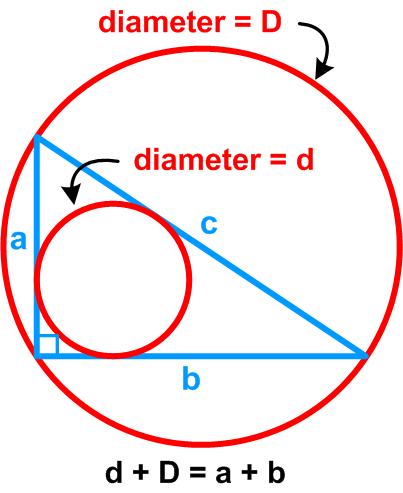
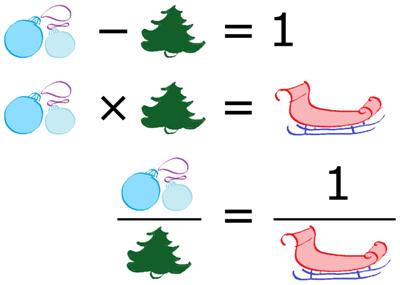 This is a slightly different mystery number puzzle from the December 2023
This is a slightly different mystery number puzzle from the December 2023  This is a slightly different type of a mixture problem from Dan Griller.
This is a slightly different type of a mixture problem from Dan Griller.