 Here is another Presh Talwalkar problem that seems unsolvable at first glance.
Here is another Presh Talwalkar problem that seems unsolvable at first glance.
“Every day, a train passes a train station along a straight line track, and the train moves at a constant speed. Two friends, A and B, want to determine how long the train is. Lacking proper equipment, they devise the following method. They first synchronize their walking. Both A and B walk at the same constant speed, and each step they take is the same length. One day they line up back to back at the train station. When the front of the train reaches them, they both start walking in opposite directions. Each person stops exactly as the back of the train passes by. If person A takes 30 steps, and person B takes 45 steps, how long is the train, in terms of steps?”
Answer.
See the Train Length Puzzle for a solution.
 This is a fun little problem from the United Kingdom Mathematics Trust (UKMT) Senior Math Challenge of 2008.
This is a fun little problem from the United Kingdom Mathematics Trust (UKMT) Senior Math Challenge of 2008.
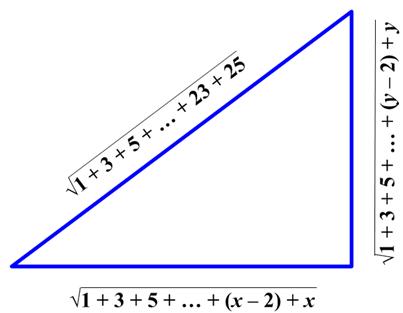 This is an interesting problem from the United Kingdom Mathematics Trust (UKMT) Senior Math Challenge of 2008.
This is an interesting problem from the United Kingdom Mathematics Trust (UKMT) Senior Math Challenge of 2008. This turns out to be a fairly challenging driving problem from Longley-Cook.
This turns out to be a fairly challenging driving problem from Longley-Cook. When our daughter-in-law made wheat shocks as center-pieces for hers and our son’s fall-themed wedding reception, I naturally could not help pointing out the age-old observation that they represented a hyperboloid of one sheet. This was naturally greeted with the usual groans, but the thought stayed with me as I realized I had never proved this mathematically to myself. And so I did.
When our daughter-in-law made wheat shocks as center-pieces for hers and our son’s fall-themed wedding reception, I naturally could not help pointing out the age-old observation that they represented a hyperboloid of one sheet. This was naturally greeted with the usual groans, but the thought stayed with me as I realized I had never proved this mathematically to myself. And so I did. Here is another Presh Talwalkar problem that seems unsolvable at first glance.
Here is another Presh Talwalkar problem that seems unsolvable at first glance.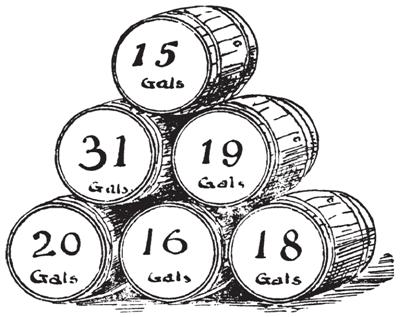 This is a great puzzle by H. E. Dudeney involving a very useful technique.
This is a great puzzle by H. E. Dudeney involving a very useful technique.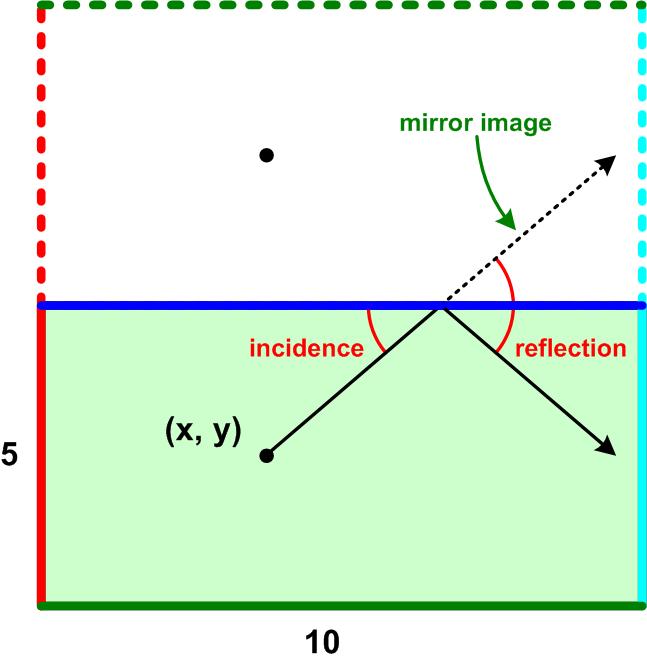 Futility Closet offers another interesting puzzle:
Futility Closet offers another interesting puzzle: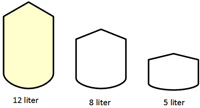 I was sifting back through some problems posed by Presh Talwalkar on his website
I was sifting back through some problems posed by Presh Talwalkar on his website 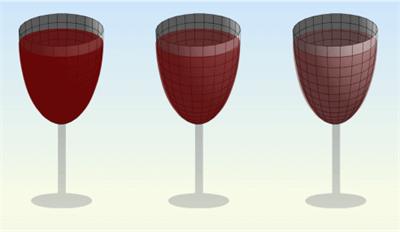 This was a rather intricate puzzle from Presh Talwalkar. I found his solution a bit hard to follow, so I tried for a clearer presentation.
This was a rather intricate puzzle from Presh Talwalkar. I found his solution a bit hard to follow, so I tried for a clearer presentation.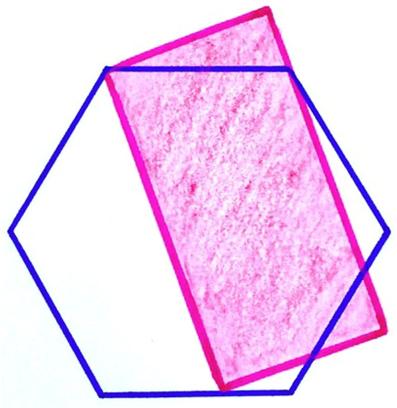 This is another interesting problem from
This is another interesting problem from