 This is a problem from the 2000 Olymon (the Mathematics Olympiads Correspondence Program) for secondary students sponsored jointly by the Canadian Mathematical Society and the Mathematics Department of the University of Toronto.
This is a problem from the 2000 Olymon (the Mathematics Olympiads Correspondence Program) for secondary students sponsored jointly by the Canadian Mathematical Society and the Mathematics Department of the University of Toronto.![]()
Find the value of S.”
See Astronomical Sum for solutions.

 This is another challenging sum from the 2024 Math Calendar.
This is another challenging sum from the 2024 Math Calendar.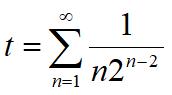 ”
” Here is a fairly computationally challenging 1994 AIME problem .
Here is a fairly computationally challenging 1994 AIME problem . Well, I discovered that the 2024 Math Calendar has some interesting problems, so I guess things will limp along for a while. This is a challenging but imaginative problem from the calendar.
Well, I discovered that the 2024 Math Calendar has some interesting problems, so I guess things will limp along for a while. This is a challenging but imaginative problem from the calendar.
 This is yet another series offered by
This is yet another series offered by 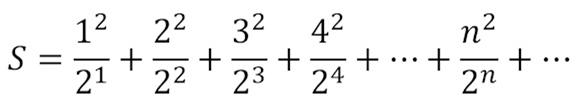
 Here is another typical sum puzzle from Presh Talwalkar.
Here is another typical sum puzzle from Presh Talwalkar. This is another stimulating little problem from the 2022 Math Calendar.
This is another stimulating little problem from the 2022 Math Calendar. This is another infinite series from
This is another infinite series from  This is a belated Christmas puzzle from December 2019
This is a belated Christmas puzzle from December 2019  Here is another sum problem, this time from the 2021 Math Calendar.
Here is another sum problem, this time from the 2021 Math Calendar.