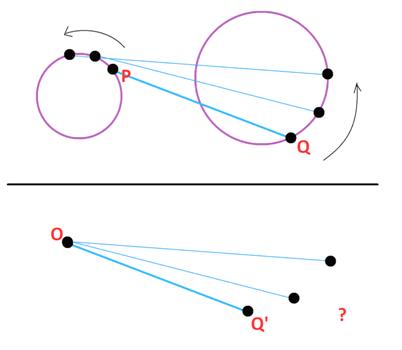
 This is one of H. E. Dudeney’s train puzzles.
This is one of H. E. Dudeney’s train puzzles.
“Two railway trains, one four hundred feet long and the other two hundred feet long, ran on parallel rails. It was found that when they went in opposite directions they passed each other in five seconds, but when they ran in the same direction the faster train would pass the other in fifteen seconds. A curious passenger worked out from these facts the rate per hour at which each train ran. Can the reader discover the correct answer? Of course, each train ran with a uniform velocity.”
See Two Trains – Passing in the Night for a solution.

 This is one the best articles I have read on gerrymandering regarding its political import, and of course it is by one of the most articulate mathematicians, Jordan Ellenberg:
This is one the best articles I have read on gerrymandering regarding its political import, and of course it is by one of the most articulate mathematicians, Jordan Ellenberg: One of the all-time examples of chance intervening in history is Christopher Columbus’s putative discovery of America. Moreover, the legend of this discovery is filled with erroneous information that was traditionally foisted upon unsuspecting elementary school children. One of the most egregious errors was the assertion that Columbus was trying to prove the earth was round and not flat. I had a picture book when I was young that showed sailors tumbling off the edge of a flat earth.
One of the all-time examples of chance intervening in history is Christopher Columbus’s putative discovery of America. Moreover, the legend of this discovery is filled with erroneous information that was traditionally foisted upon unsuspecting elementary school children. One of the most egregious errors was the assertion that Columbus was trying to prove the earth was round and not flat. I had a picture book when I was young that showed sailors tumbling off the edge of a flat earth. This essay introduces a topic I have been thinking about for a number of years. It also may allow me to connect the math impulse to a wider range of thoughts than just those based on math or even science.
This essay introduces a topic I have been thinking about for a number of years. It also may allow me to connect the math impulse to a wider range of thoughts than just those based on math or even science.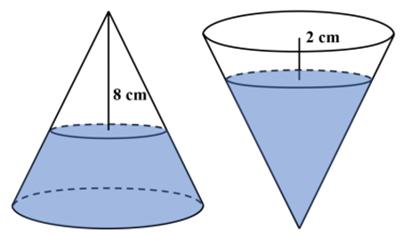 I was astonished that this problem was suitable for 8th graders. First of all the formula for the volume of a cone is one of the least-remembered of formulas, and I certainly never remember it. So my only viable approach was calculus, which is probably not a suitable solution for an 8th grader.
I was astonished that this problem was suitable for 8th graders. First of all the formula for the volume of a cone is one of the least-remembered of formulas, and I certainly never remember it. So my only viable approach was calculus, which is probably not a suitable solution for an 8th grader.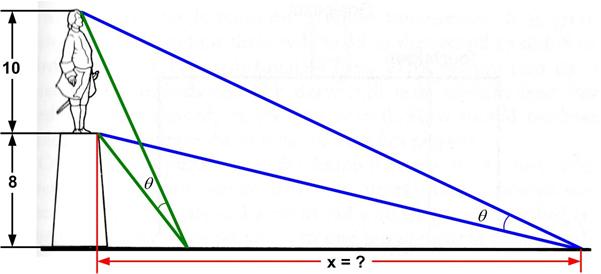 This is an old problem I had seen before. Here is David Wells’s rendition:
This is an old problem I had seen before. Here is David Wells’s rendition: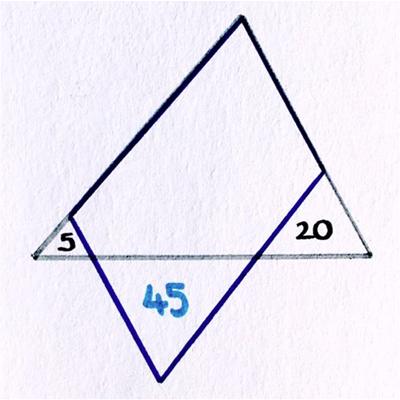
 A mathematics friend of mine just sent me this link to a 2017
A mathematics friend of mine just sent me this link to a 2017