 The subtext of this essay might be “word problems,” since the stream of thoughts that led to the za’irajah (zairja) began with a paper I read, while searching for potential problems for this website, on the history of word problems in high school texts in algebra in the 20th and 21st centuries. The following statement by Lorenat caught my attention:
The subtext of this essay might be “word problems,” since the stream of thoughts that led to the za’irajah (zairja) began with a paper I read, while searching for potential problems for this website, on the history of word problems in high school texts in algebra in the 20th and 21st centuries. The following statement by Lorenat caught my attention:
“The newer characteristics of how word problems are treated in Long’s text [2016] … include adding sympathetic commentary about fear of word problems. ‘And of course, there are those dreaded “Word Problems,” but I’ve solved them all for you, so they’re painless.’
[Lorenat continues,] A more extreme example of this is exhibited in the word problem commentary of Michael W. Kelley’s The Idiot’s Complete Guide to Algebra: Second Edition from 2007, in which he describes word problems as ‘a necessary evil of algebra, jammed in there to show you that you can use algebra in “real life.”’ However, Kelley makes no attempt to write ‘real life’ word problems, and criticizes the uselessness of the word problems he does include.”
This essay is an attempt to rebut such negative views of solving word problems by placing the activity in a more favorable historical context.
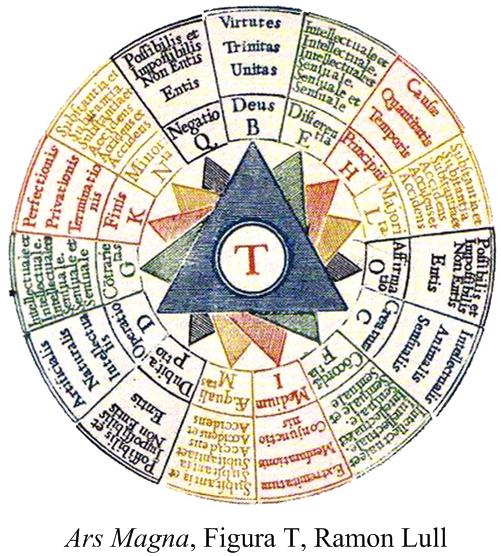
See the Za’irajah and Mathematics
 I have been meaning to focus on this aspect of mathematics for some time. It is a topic I elaborated in my “Angular Momentum” post. But I also think it has something to do with the difficulties that normal folks have with elementary math, in particular, numbers. I thought I would dub it the Cheshire Cat Paradigm, involving the Cheshire Cat’s grin.
I have been meaning to focus on this aspect of mathematics for some time. It is a topic I elaborated in my “Angular Momentum” post. But I also think it has something to do with the difficulties that normal folks have with elementary math, in particular, numbers. I thought I would dub it the Cheshire Cat Paradigm, involving the Cheshire Cat’s grin.
 In one of our periodic FaceTime calls I found out that my granddaughter in 6th grade was interested in learning algebra and had gotten a book to help her out. Clearly this initiative to get a head start prior to the normal course curriculum excited me, so I wrote what I thought was an insightful essay on the meaning and purpose of algebra. Needless to say it was an abysmal failure.
In one of our periodic FaceTime calls I found out that my granddaughter in 6th grade was interested in learning algebra and had gotten a book to help her out. Clearly this initiative to get a head start prior to the normal course curriculum excited me, so I wrote what I thought was an insightful essay on the meaning and purpose of algebra. Needless to say it was an abysmal failure. A prevalent theme of much of popular mathematical exposition and debates about mathematics education concerns how to interest a wider population in matters mathematical. For the most part I feel that essays that try to present the “beauty” of mathematics are doomed to failure, as are most discussions of esthetics. The underlying goal of such writing is a legitimate and laudable attempt to show the appeal of math. But I fear it succeeds only with those already converted. So is there another way?
A prevalent theme of much of popular mathematical exposition and debates about mathematics education concerns how to interest a wider population in matters mathematical. For the most part I feel that essays that try to present the “beauty” of mathematics are doomed to failure, as are most discussions of esthetics. The underlying goal of such writing is a legitimate and laudable attempt to show the appeal of math. But I fear it succeeds only with those already converted. So is there another way?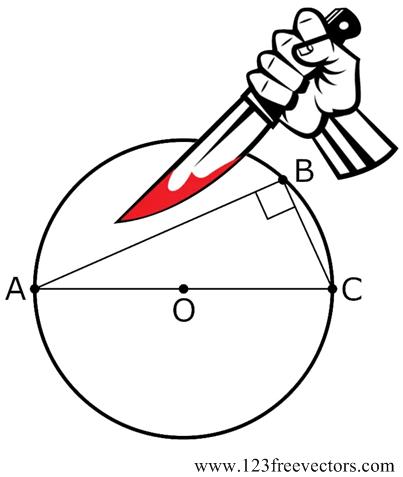 One of my favorite bloggers, Kevin Drum, decided to relieve the tedium of our current political anarchy by whacking the hornets’ nest of the high school mathematics curriculum, in particular the subject of plane geometry. You can tell from the tag list on my blog that I hold plane geometry in high regard and can’t let this gibe pass without some rebuttal, futile as it may be. Actually, I am not going to weigh in on the general issue of the current math curriculum that much, but rather make a few observations from my own experience over the years as it relates to
One of my favorite bloggers, Kevin Drum, decided to relieve the tedium of our current political anarchy by whacking the hornets’ nest of the high school mathematics curriculum, in particular the subject of plane geometry. You can tell from the tag list on my blog that I hold plane geometry in high regard and can’t let this gibe pass without some rebuttal, futile as it may be. Actually, I am not going to weigh in on the general issue of the current math curriculum that much, but rather make a few observations from my own experience over the years as it relates to  Given the aggravating times, I thought I would vent my frustration by ranting on a somewhat nonsensical topic: “The fact that the earth revolves around the sun, rather than the sun around the earth.” This assertion is often used to separate the supposed dunces from the enlightened. It is put on the same level as “the fact that the earth is round (a sphere) and not flat” with the dunces labeled “flat-earthers.”
Given the aggravating times, I thought I would vent my frustration by ranting on a somewhat nonsensical topic: “The fact that the earth revolves around the sun, rather than the sun around the earth.” This assertion is often used to separate the supposed dunces from the enlightened. It is put on the same level as “the fact that the earth is round (a sphere) and not flat” with the dunces labeled “flat-earthers.” The subtext of this essay might be “word problems,” since the stream of thoughts that led to the za’irajah (zairja) began with a paper I read, while searching for potential problems for this website, on the history of word problems in high school texts in algebra in the 20th and 21st centuries. The following statement by Lorenat caught my attention:
The subtext of this essay might be “word problems,” since the stream of thoughts that led to the za’irajah (zairja) began with a paper I read, while searching for potential problems for this website, on the history of word problems in high school texts in algebra in the 20th and 21st centuries. The following statement by Lorenat caught my attention: One of the books that has stuck with me over the years is Carl Becker’s The Declaration of Independence (1922, reprint 1942), not only for its incredibly clear and beautiful writing but also for its emphasis on the impact of the revolution most prominently caused by Isaac Newton, which was later subsumed under the term Scientific Revolution covering the entire 17th century. A consequence of this remarkable period was the so-called Enlightenment that followed in the 18th century and became the soil from which our nation’s founding ideas and documents sprang. Both these centuries have been further optimistically called the Age of Reason.
One of the books that has stuck with me over the years is Carl Becker’s The Declaration of Independence (1922, reprint 1942), not only for its incredibly clear and beautiful writing but also for its emphasis on the impact of the revolution most prominently caused by Isaac Newton, which was later subsumed under the term Scientific Revolution covering the entire 17th century. A consequence of this remarkable period was the so-called Enlightenment that followed in the 18th century and became the soil from which our nation’s founding ideas and documents sprang. Both these centuries have been further optimistically called the Age of Reason. It is a bit presumptuous to think I could reduce the universe of mathematics to some succinct essence, but ever since I first saw a column in Martin Gardner’s Scientific American Mathematical Games in 1967, I thought his example illustrated the essential feature of mathematics, or at least one of its principal attributes. And he posed it in a way that would be accessible to anyone. I especially wanted to credit Martin Gardner, since the idea resurfaced recently, uncredited, in some attractive videos by Katie Steckles and James Grime. (This reminds me of the Borges idea that “eighty years of oblivion are perhaps equal to novelty”.) See the
It is a bit presumptuous to think I could reduce the universe of mathematics to some succinct essence, but ever since I first saw a column in Martin Gardner’s Scientific American Mathematical Games in 1967, I thought his example illustrated the essential feature of mathematics, or at least one of its principal attributes. And he posed it in a way that would be accessible to anyone. I especially wanted to credit Martin Gardner, since the idea resurfaced recently, uncredited, in some attractive videos by Katie Steckles and James Grime. (This reminds me of the Borges idea that “eighty years of oblivion are perhaps equal to novelty”.) See the  This subject admittedly has only a tenuous relationship to mathematics (via arithmetic), but perhaps it can join more mathematically challenging political topics like voting and gerrymandering. In any case, I was stimulated to consider the idea of reapportioning the US Senate by the % US population of each state by an 8 December 2018 article in the Atlantic by former Congressman John Dingell, who advocated abolishing the Senate. I thought this a bit too Draconian and considered the percent population idea as a better compromise. It turned out I was not alone in having this (obvious) thought: I just came across a more extensive 2 January 2019 Atlantic article by Eric Orts that concurs with my idea about reapportionment of the Senate, discusses the legal ramifications in more detail, and echoes the benefits I mentioned as well as others. See
This subject admittedly has only a tenuous relationship to mathematics (via arithmetic), but perhaps it can join more mathematically challenging political topics like voting and gerrymandering. In any case, I was stimulated to consider the idea of reapportioning the US Senate by the % US population of each state by an 8 December 2018 article in the Atlantic by former Congressman John Dingell, who advocated abolishing the Senate. I thought this a bit too Draconian and considered the percent population idea as a better compromise. It turned out I was not alone in having this (obvious) thought: I just came across a more extensive 2 January 2019 Atlantic article by Eric Orts that concurs with my idea about reapportionment of the Senate, discusses the legal ramifications in more detail, and echoes the benefits I mentioned as well as others. See 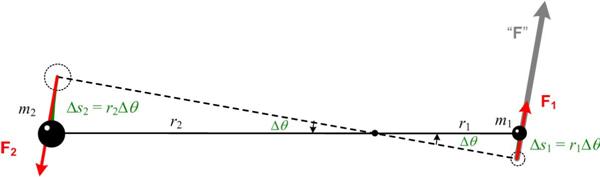 I have always had a tenuous relationship with the concept of angular momentum, but recently my concerns resurfaced when I did my studies on Kepler, and in particular his
I have always had a tenuous relationship with the concept of angular momentum, but recently my concerns resurfaced when I did my studies on Kepler, and in particular his