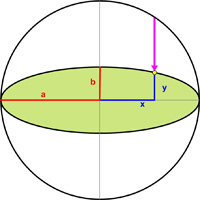
 I had been exploring how Kepler originally discovered his first two laws and became fascinated by what he did in his Astronomia Nova (1609), as presented by a number of researchers. Among the writers was A. E. L. Davis. She mentioned that the characterization of the ellipse that Kepler was using was the idea of a “compressed circle,” that is, a circle all of whose points were shrunk vertically by a constant amount towards a fixed diameter of the circle. I did not recall ever hearing this idea before and tried to track down its origin together with a proof — futilely, Davis’s references notwithstanding. I then tried to prove it myself. It was easy to do with analytic geometry. But in the spirit of the Kepler era (before the advent of Fermat’s and Descartes’s beginnings at fusing algebra and geometry) I tried to prove it solely within Euclid’s plane geometry. Some critical steps seemed to come from the great work of Apollonius of Perga (262-190 BC) on Conics. But for me a final elegant proof was not evident until 1822 when Dandelin employed his inscribed spheres. See Kepler’s Ellipse.
I had been exploring how Kepler originally discovered his first two laws and became fascinated by what he did in his Astronomia Nova (1609), as presented by a number of researchers. Among the writers was A. E. L. Davis. She mentioned that the characterization of the ellipse that Kepler was using was the idea of a “compressed circle,” that is, a circle all of whose points were shrunk vertically by a constant amount towards a fixed diameter of the circle. I did not recall ever hearing this idea before and tried to track down its origin together with a proof — futilely, Davis’s references notwithstanding. I then tried to prove it myself. It was easy to do with analytic geometry. But in the spirit of the Kepler era (before the advent of Fermat’s and Descartes’s beginnings at fusing algebra and geometry) I tried to prove it solely within Euclid’s plane geometry. Some critical steps seemed to come from the great work of Apollonius of Perga (262-190 BC) on Conics. But for me a final elegant proof was not evident until 1822 when Dandelin employed his inscribed spheres. See Kepler’s Ellipse.
In the process of exploring the compressed circle idea I acquired an immense appreciation and regard for Kepler and his perseverance in the face of the dominant paradigm of his era, namely, the 2000 year old idea that the celestial motions were all based on the most perfect motion of all, that of circles. The kinds of extremely laborious calculations he went through (just prior to the invention of logarithms by John Napier) were daunting, especially considering the trials he was undergoing in his personal life (trying to survive the religious destruction between Catholics and Protestants, along with defending his mother against charges of witchcraft).

 Years ago (1963) I got the paperback The Calculus:A Genetic Approach, by Otto Toeplitz, which presented the basic ideas of the differential and integral calculus from a historical point of view. One thing Toeplitz did at the end of his book that I had not seen in other texts was to show the equivalence of Kepler’s Laws and Newton’s Law of Gravity. (Since 1963 David Bressoud has developed this theme in his excellent 1991 text.) I thought I would try to emulate Toeplitz’s approach with more modern notation (vectors) and arguments in hopes of extracting the essential ideas from the clutter.
Years ago (1963) I got the paperback The Calculus:A Genetic Approach, by Otto Toeplitz, which presented the basic ideas of the differential and integral calculus from a historical point of view. One thing Toeplitz did at the end of his book that I had not seen in other texts was to show the equivalence of Kepler’s Laws and Newton’s Law of Gravity. (Since 1963 David Bressoud has developed this theme in his excellent 1991 text.) I thought I would try to emulate Toeplitz’s approach with more modern notation (vectors) and arguments in hopes of extracting the essential ideas from the clutter. This is another problem from the
This is another problem from the 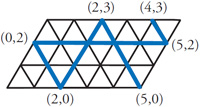 Years ago (1967) I read about an interesting solution to the three jugs problem in a book by Nathan Court which involved the idea of a billiard ball traversing a skew billiard table with distributions of the water between the jugs listed along the edges of the table. The ball bounced between solutions until it ended on the desired value. I thought it was very clever, but I really did not understand why it worked. Later I figured out an explanation, which I present here. See the
Years ago (1967) I read about an interesting solution to the three jugs problem in a book by Nathan Court which involved the idea of a billiard ball traversing a skew billiard table with distributions of the water between the jugs listed along the edges of the table. The ball bounced between solutions until it ended on the desired value. I thought it was very clever, but I really did not understand why it worked. Later I figured out an explanation, which I present here. See the  Another good source of problems is the
Another good source of problems is the 
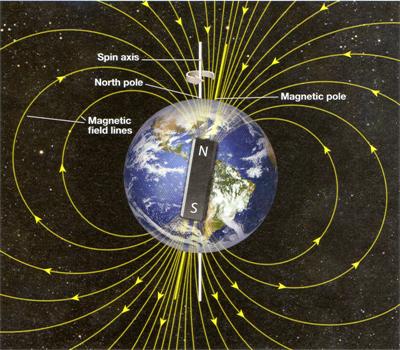 This was one of my more satisfying essays. Several years ago I gave some thought to what it meant for the earth to be considered a magnet. More recently in 2012 an article in the magazine BirdWatching brought it all back when I saw its diagram of the earth as a magnet for guiding migratory birds. Knowing that magnets have north and south poles, where should we expect to find the earth’s north and south magnetic poles? See
This was one of my more satisfying essays. Several years ago I gave some thought to what it meant for the earth to be considered a magnet. More recently in 2012 an article in the magazine BirdWatching brought it all back when I saw its diagram of the earth as a magnet for guiding migratory birds. Knowing that magnets have north and south poles, where should we expect to find the earth’s north and south magnetic poles? See 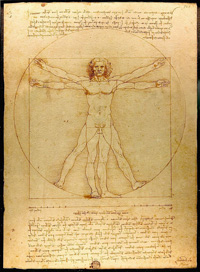 This is a mildly pointless 2015 article about Leonardo Da Vinci’s famous drawing of the Vitruvian Man spread-eagled and inscribed in a circle and a square. I started wondering about the positions and whether they over-determined the circle and square. What hidden constraints were being assumed? One assumption turned out to be famous, namely, that the height of a man equaled the distance between his finger tips when he holds his arms straight out to either side of his body. I had been told this in childhood, and I never knew where it came from. Also, I don’t think it is true in every case (what about women?), though it does appear to be close (and is true in my case). See the
This is a mildly pointless 2015 article about Leonardo Da Vinci’s famous drawing of the Vitruvian Man spread-eagled and inscribed in a circle and a square. I started wondering about the positions and whether they over-determined the circle and square. What hidden constraints were being assumed? One assumption turned out to be famous, namely, that the height of a man equaled the distance between his finger tips when he holds his arms straight out to either side of his body. I had been told this in childhood, and I never knew where it came from. Also, I don’t think it is true in every case (what about women?), though it does appear to be close (and is true in my case). See the 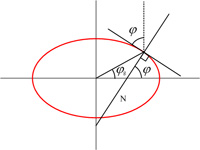
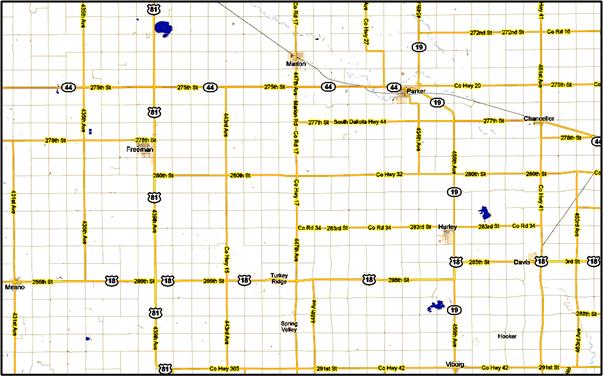 This light-weight problem arose from a newspaper article that had me looking at a Google map of the area near Sioux Falls, South Dakota. What I saw was an excellent example of the Taxicab Geometry, allegedly first considered by Hermann Minkowski, mathematical friend of Albert Einstein. The map configuration was perpetrated by the great Public Land Survey System (PLSS) that originated with Thomas Jefferson and spread from Ohio (more or less) west to the California coast. This scheme overlaid the country basically with a 1 mile x 1 mile square grid of roads, and South Dakota is a prime example.
This light-weight problem arose from a newspaper article that had me looking at a Google map of the area near Sioux Falls, South Dakota. What I saw was an excellent example of the Taxicab Geometry, allegedly first considered by Hermann Minkowski, mathematical friend of Albert Einstein. The map configuration was perpetrated by the great Public Land Survey System (PLSS) that originated with Thomas Jefferson and spread from Ohio (more or less) west to the California coast. This scheme overlaid the country basically with a 1 mile x 1 mile square grid of roads, and South Dakota is a prime example.