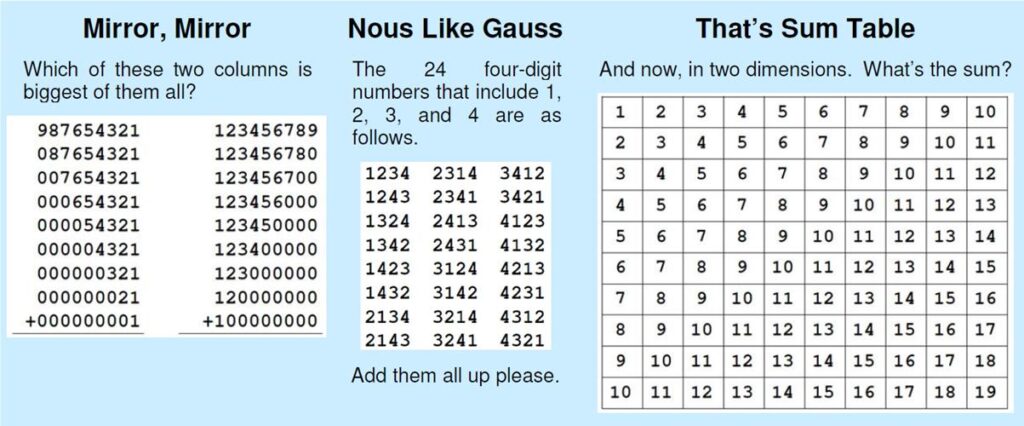
This is a recent Alex Bellos problem that supposedly can be solved by 12-year-olds!
This is a recent Alex Bellos problem that supposedly can be solved by 12-year-olds!
“Today’s problems come from Axiom Maths, a charity that that takes high-attaining primary school children and provides them with maths enrichment during secondary school.
One of Axiom’s main activities is to organise ‘maths circles’, in which small groups of pupils get together to tackle fun problems. Such as the ones below, which are aimed at children aged 11/12, and form the basis for further explorations.
Really Secret Santa
A group of nine secret agents: 001, 002, 003, 004, 005, 006, 007, 008 and 009 have organised a Secret Santa. The instructions are coded, to keep the donors secret.
- Agent 001 gives a present to the agent who gives a present to agent 002
- Agent 002 gives a present to the agent who gives a present to agent 003
- Agent 003 gives a present to the agent who gives a present to agent 004
- and so on, until
- Agent 009 gives a present to the agent who gives a present to agent 001
Which agent will agent 007 get her present from?”
See the Spy Gift Problem for solutions.

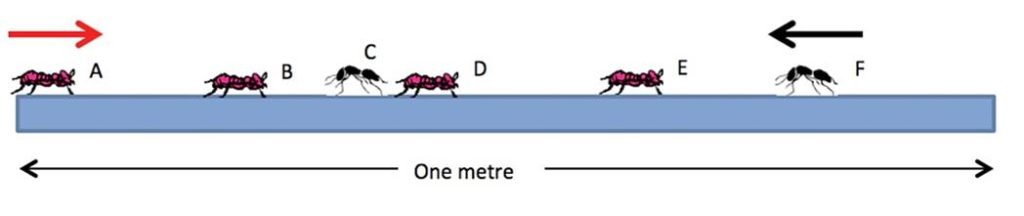
 For his Monday Puzzle in the Guardian Alex Bellos provided a seemingly impossible
For his Monday Puzzle in the Guardian Alex Bellos provided a seemingly impossible 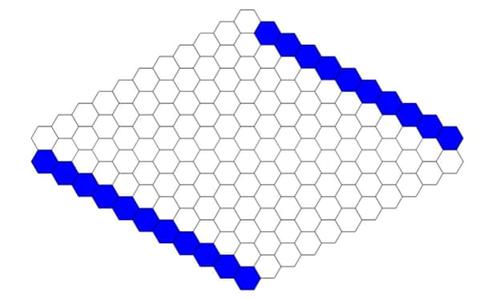
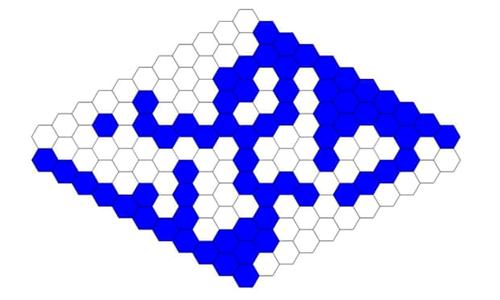
 Unfortunately Ukraine has receded from our attention under the threat from our own anti-democratic forces, but this
Unfortunately Ukraine has receded from our attention under the threat from our own anti-democratic forces, but this 
 This is a fairly straight-forward logic
This is a fairly straight-forward logic  This
This 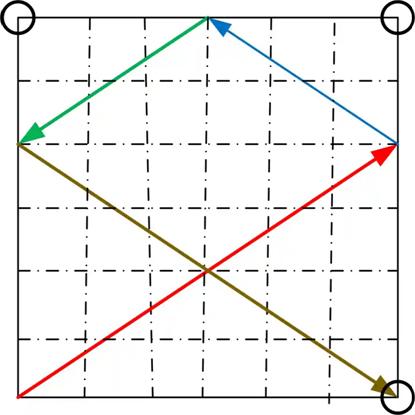 This is a nice
This is a nice  For a change of pace, here is an early
For a change of pace, here is an early