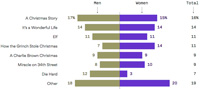
 Reading Axios on Christmas Eve day 2017, I was struck by what appeared at first to be a strange graph showing preferences for Christmas movies divided between men and women. The thing that struck me as strange was the computation for the total votes: the percentages were the average of the men and women percentages. This, of course, is not how you average percentages. What was going on? See Strange Statistics.
Reading Axios on Christmas Eve day 2017, I was struck by what appeared at first to be a strange graph showing preferences for Christmas movies divided between men and women. The thing that struck me as strange was the computation for the total votes: the percentages were the average of the men and women percentages. This, of course, is not how you average percentages. What was going on? See Strange Statistics.
Monthly Archives: December 2018
Tupper’s Self-Referential Formula
![]() Recently I viewed a startling video by Matt Parker about the Tupper Self-Referential Formula. It is a formula that visually represents itself when graphed at a specific location in the (x, y) plane. I found it difficult to fathom, so I looked it up on Wikipedia and Google. After reading different explanations, I finally think I have the idea. So thought I would add my version to the mix. See Tupper Self-Referential Formula.
Recently I viewed a startling video by Matt Parker about the Tupper Self-Referential Formula. It is a formula that visually represents itself when graphed at a specific location in the (x, y) plane. I found it difficult to fathom, so I looked it up on Wikipedia and Google. After reading different explanations, I finally think I have the idea. So thought I would add my version to the mix. See Tupper Self-Referential Formula.
Corner Reflectors
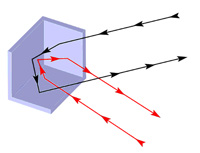 I came across the following entry in the Futility Closet website that cried out for justification. “An arrangement of three mutually perpendicular planes, like those in the corner of a cube, have a pleasing property: They’ll reflect a ray of light back in the direction that it came from.” So the question is, why is this reflection property true? See Corner Reflectors.
I came across the following entry in the Futility Closet website that cried out for justification. “An arrangement of three mutually perpendicular planes, like those in the corner of a cube, have a pleasing property: They’ll reflect a ray of light back in the direction that it came from.” So the question is, why is this reflection property true? See Corner Reflectors.
The Pythagorean Theorem
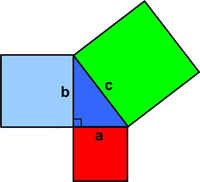 All too frequently I come across the usual statements questioning why non-technical folks should bother studying math. A typical example is the Pythagorean Theorem. People say, “What good is that? I’ll never use it. So why bother?” Ah, the famous “utility” argument – as if everything worthwhile must be “useful.” I thought I would take this “useless” math example par excellence and show that, in fact, it harbors many of the best aspects of mathematics that anyone should find appealing. See the Pythagorean Theorem
All too frequently I come across the usual statements questioning why non-technical folks should bother studying math. A typical example is the Pythagorean Theorem. People say, “What good is that? I’ll never use it. So why bother?” Ah, the famous “utility” argument – as if everything worthwhile must be “useful.” I thought I would take this “useless” math example par excellence and show that, in fact, it harbors many of the best aspects of mathematics that anyone should find appealing. See the Pythagorean Theorem
Slow Lane Problem
![]() Paul Krugman in his 26 July 2013 New York Times column “The Conscience of a Liberal” provided an analysis about why we are always being caught in the slow lane of a congested highway. I tried to fill in the gaps in his laconic explanation. See the Slow Lane Problem.
Paul Krugman in his 26 July 2013 New York Times column “The Conscience of a Liberal” provided an analysis about why we are always being caught in the slow lane of a congested highway. I tried to fill in the gaps in his laconic explanation. See the Slow Lane Problem.
The Two Errand Boys
 This is another puzzle from the Futility Closet that was originally from Henry Dudeney’s Canterbury Puzzles.
This is another puzzle from the Futility Closet that was originally from Henry Dudeney’s Canterbury Puzzles.
“A country baker sent off his boy with a message to the butcher in the next village, and at the same time the butcher sent his boy to the baker. One ran faster than the other, and they were seen to pass at a spot 720 yards from the baker’s shop. Each stopped ten minutes at his destination and then started on the return journey, when it was found that they passed each other at a spot 400 yards from the butcher’s. How far apart are the two tradesmen’s shops? Of course each boy went at a uniform pace throughout.”
See the Two Errand Boys for solutions.
Mercator Projection Balloon
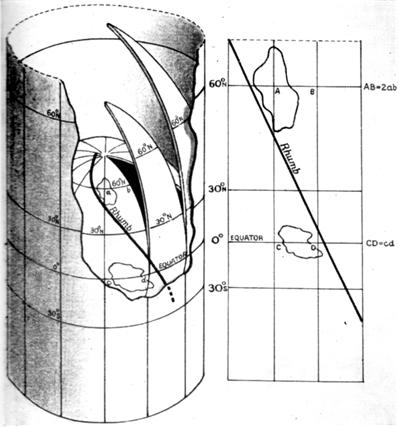 Years ago during one of my many excursions into the history of mathematics I wondered how Mercator used logarithms in his map projection (introduced in a 1569 map) when logarithms were not discovered by John Napier (1550-1617) and published in his book Mirifici Logarithmorum Canonis Descriptio until 1614, three years before his death in 1617. The mystery was solved when I read a 1958 book by D. W. Waters which said Edward Wright (1561-1615) in his 1599 book Certaine Errors in Navigation produced his “most important correction, his chart projection, now known as Mercator’s.” Wright did not use logarithms explicitly but rather implicitly through the summing of discrete secants of the latitude as scale factors. But what really caught my attention in the Waters book was this arresting footnote: “Wright explained his projection in terms of a bladder blown up inside a cylinder, a very good analogy.” This article recounts my exploration of this idea. See Mercator Projection Balloon.
Years ago during one of my many excursions into the history of mathematics I wondered how Mercator used logarithms in his map projection (introduced in a 1569 map) when logarithms were not discovered by John Napier (1550-1617) and published in his book Mirifici Logarithmorum Canonis Descriptio until 1614, three years before his death in 1617. The mystery was solved when I read a 1958 book by D. W. Waters which said Edward Wright (1561-1615) in his 1599 book Certaine Errors in Navigation produced his “most important correction, his chart projection, now known as Mercator’s.” Wright did not use logarithms explicitly but rather implicitly through the summing of discrete secants of the latitude as scale factors. But what really caught my attention in the Waters book was this arresting footnote: “Wright explained his projection in terms of a bladder blown up inside a cylinder, a very good analogy.” This article recounts my exploration of this idea. See Mercator Projection Balloon.
(Update 4/2/2022) Balloon Idea as Rubberband
 Imagine my surprise when I realized Burkard Polster’s latest Mathologer post “The magic log wheel: How was this missed for 400 years?” involving a circular sliderule presented the logarithm effect as stretching a rubberband around a circle. This is essentially the balloon effect only sort of in reverse.
Imagine my surprise when I realized Burkard Polster’s latest Mathologer post “The magic log wheel: How was this missed for 400 years?” involving a circular sliderule presented the logarithm effect as stretching a rubberband around a circle. This is essentially the balloon effect only sort of in reverse.
Lambert Equal-Area Cylindrical Map Projection
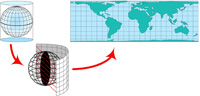 One thing I have always been curious about, but never got around to investigating, is how hard is it to see that the Lambert Equal-Area Projection of a sphere onto a cylinder in fact preserves areas? This 2012 essay attempts to provide an answer. The essay was recently updated to provide a link to the fabulous Youtube site by Grant Sanderson at 3blue1brown. He shows a different way of looking at the problem also without explicitly resorting to calculus. All his videos are spectacular and provide unparalleled insights into mathematics. What I wouldn’t give to have had such videos available when I was studying math. How much more quickly would I have been able to learn. See Lambert Equal Area Projection.
One thing I have always been curious about, but never got around to investigating, is how hard is it to see that the Lambert Equal-Area Projection of a sphere onto a cylinder in fact preserves areas? This 2012 essay attempts to provide an answer. The essay was recently updated to provide a link to the fabulous Youtube site by Grant Sanderson at 3blue1brown. He shows a different way of looking at the problem also without explicitly resorting to calculus. All his videos are spectacular and provide unparalleled insights into mathematics. What I wouldn’t give to have had such videos available when I was studying math. How much more quickly would I have been able to learn. See Lambert Equal Area Projection.
Cutting Elliptical Pizza into Equal Slices
 Having immersed myself in studying Kepler’s discovery that the planetary orbits were ellipses, I was immediately aware of how the British mathematician, Katie Steckles, justified her technique to cut an elliptical pizza into equal slices in her video of 14 March 2017. In her video Katie makes the claim that the result of any affine transformation of the circular pizza cut into equal sectors will also be a set of equal area slices. I made an attempt to substantiate these remarks. See Cutting Elliptical Pizza.
Having immersed myself in studying Kepler’s discovery that the planetary orbits were ellipses, I was immediately aware of how the British mathematician, Katie Steckles, justified her technique to cut an elliptical pizza into equal slices in her video of 14 March 2017. In her video Katie makes the claim that the result of any affine transformation of the circular pizza cut into equal sectors will also be a set of equal area slices. I made an attempt to substantiate these remarks. See Cutting Elliptical Pizza.
Kepler’s Equal Areas Law
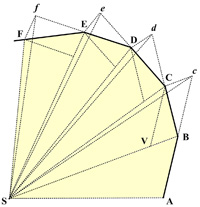 I have long been fascinated by Newton’s proof of Kepler’s Equal Areas Law and wanted to write about it. Of course, others have as well, but I wanted to emphasize an aspect of the proof that supported my philosophy of mathematics.
I have long been fascinated by Newton’s proof of Kepler’s Equal Areas Law and wanted to write about it. Of course, others have as well, but I wanted to emphasize an aspect of the proof that supported my philosophy of mathematics.
Before I get to Newton, however, I wanted to discuss how Kepler himself justified this law, since his approach has a number of fascinating historical aspects to it. I have previously discussed Kepler’s ellipse and in the process of doing that research, I came across a number of articles about how Kepler arrived at his equal areas law. One notable result is that even though now we call the idea that a planet orbits the Sun in an elliptical path with the Sun at one focus, Kepler’s First Law, and the idea that the line from the Sun to the planet sweeps out equal areas in equal times, Kepler’s Second Law, Kepler actually discovered these laws in reverse order. See Kepler’s Equal Areas Law
