 Here is a seemingly simple problem from Futility Closet.
Here is a seemingly simple problem from Futility Closet.
“A quickie from Peter Winkler’s Mathematical Puzzles, 2021: Can West Virginia be inscribed in a square? That is, is it possible to draw some square each of whose four sides is tangent to this shape?”
Technically we might rephrase this as, can we inscribe a flat map of West Virginia in a square, since the boundary of most states is probably not differentiable everywhere, that is, has a tangent everywhere.
But the real significance of the problem is that it is an example of an “existence proof”, which in mathematics refers to a proof that asserts the existence of a solution to a problem, but does not (or cannot) produce the solution itself. These proofs are second in delight only to the “impossible proofs” which prove that something is impossible, such as trisecting an angle solely with ruler and compass.
Here is another classic example (whose origin I don’t recall). Consider the temperatures of the earth around the equator. At any given instant of time there must be at least two antipodal points that have the same temperature. (Antipodal points are the opposite ends of a diameter through the center of the earth.)
See Existence Proofs (revised)
(Update 10/2/2021) I fixed a minor typo: “tail” should have been “head”
 This is another race puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings for 2013.
This is another race puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings for 2013.
 This is another puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings.
This is another puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings. This is a nice puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings.
This is a nice puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings. This is a nice puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings.
This is a nice puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings.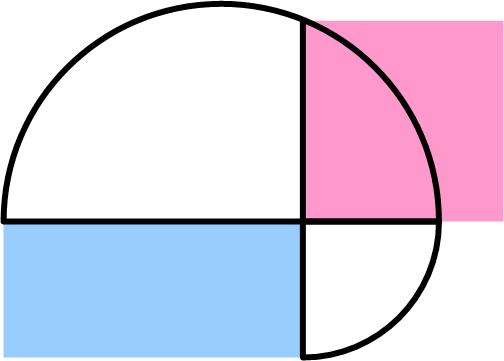 This is a provocative puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings for 2013.
This is a provocative puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings for 2013. This is an imaginative puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings for 2012.
This is an imaginative puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings for 2012. This is a thoughtful puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings.
This is a thoughtful puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings. Here is a seemingly simple problem from Futility Closet.
Here is a seemingly simple problem from Futility Closet. Years ago during one of my many excursions into the history of mathematics I wondered how Mercator used logarithms in his map projection (introduced in a 1569 map) when logarithms were not discovered by John Napier (1550-1617) and published in his book Mirifici Logarithmorum Canonis Descriptio until 1614, three years before his death in 1617. The mystery was solved when I read a 1958 book by D. W. Waters which said Edward Wright (1561-1615) in his 1599 book Certaine Errors in Navigation produced his “most important correction, his chart projection, now known as Mercator’s.” Wright did not use logarithms explicitly but rather implicitly through the summing of discrete secants of the latitude as scale factors. But what really caught my attention in the Waters book was this arresting footnote: “Wright explained his projection in terms of a bladder blown up inside a cylinder, a very good analogy.” This article recounts my exploration of this idea. See
Years ago during one of my many excursions into the history of mathematics I wondered how Mercator used logarithms in his map projection (introduced in a 1569 map) when logarithms were not discovered by John Napier (1550-1617) and published in his book Mirifici Logarithmorum Canonis Descriptio until 1614, three years before his death in 1617. The mystery was solved when I read a 1958 book by D. W. Waters which said Edward Wright (1561-1615) in his 1599 book Certaine Errors in Navigation produced his “most important correction, his chart projection, now known as Mercator’s.” Wright did not use logarithms explicitly but rather implicitly through the summing of discrete secants of the latitude as scale factors. But what really caught my attention in the Waters book was this arresting footnote: “Wright explained his projection in terms of a bladder blown up inside a cylinder, a very good analogy.” This article recounts my exploration of this idea. See 