 I have been meaning to focus on this aspect of mathematics for some time. It is a topic I elaborated in my “Angular Momentum” post. But I also think it has something to do with the difficulties that normal folks have with elementary math, in particular, numbers. I thought I would dub it the Cheshire Cat Paradigm, involving the Cheshire Cat’s grin.
I have been meaning to focus on this aspect of mathematics for some time. It is a topic I elaborated in my “Angular Momentum” post. But I also think it has something to do with the difficulties that normal folks have with elementary math, in particular, numbers. I thought I would dub it the Cheshire Cat Paradigm, involving the Cheshire Cat’s grin.
See the Cheshire Cat Paradigm.
(Updates 6/7/2025, 7/19/2025, 7/20/2025) Contra Concrete Algebra, James Tanton Videos, Imaginary Numbers Continue reading

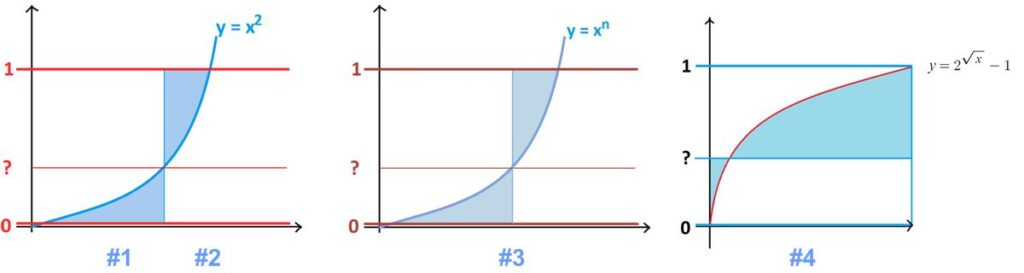 A while ago James Tanton provided a series of puzzles:
A while ago James Tanton provided a series of puzzles: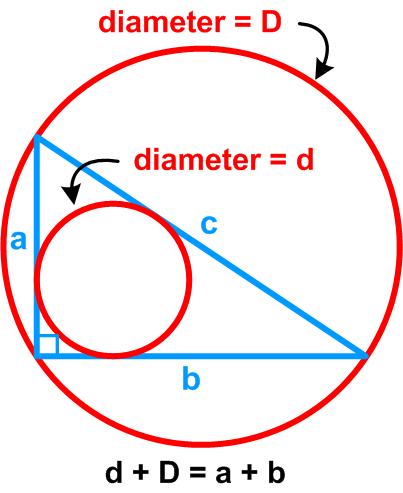
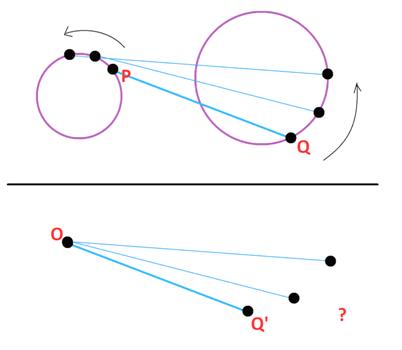
 James Tanton provides another imaginative
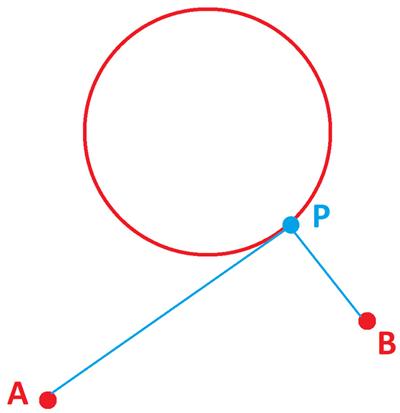
James Tanton provides another imaginative  Here is a seemingly simple problem from Futility Closet.
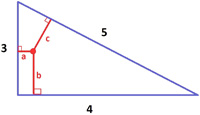
Here is a seemingly simple problem from Futility Closet.
 James Tanton
James Tanton