 This is another Futility Closet puzzle.
This is another Futility Closet puzzle.
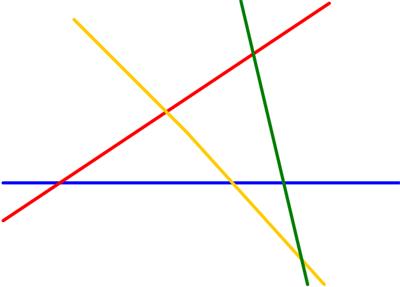
“Four straight roads cross a plain. No two are parallel, and no three meet in a point. On each road is a traveler who moves at some constant speed. If Blue and Red meet each other at their crossroad, and each of them meets Yellow and Green at their respective crossroads, will Yellow and Green necessarily meet at their own crossroad?”
I was not able to understand the solution given at first, so I tried to solve the problem on my own. Once I did, I was able to see what the Futility Closet solution was getting at. Certainly diagrams were needed to make sense of it all, and that is what I provided. See the Four Travelers Problem.

 I came across the following entry in the
I came across the following entry in the  This is another puzzle from the
This is another puzzle from the  This is another problem from the
This is another problem from the  Another good source of problems is the
Another good source of problems is the