 This turned out to be a challenging puzzle from the 1980 Canadian Math Society’s magazine, Crux Mathematicorum.
This turned out to be a challenging puzzle from the 1980 Canadian Math Society’s magazine, Crux Mathematicorum.
“Proposed by Leon Bankoff, Los Angeles, California.
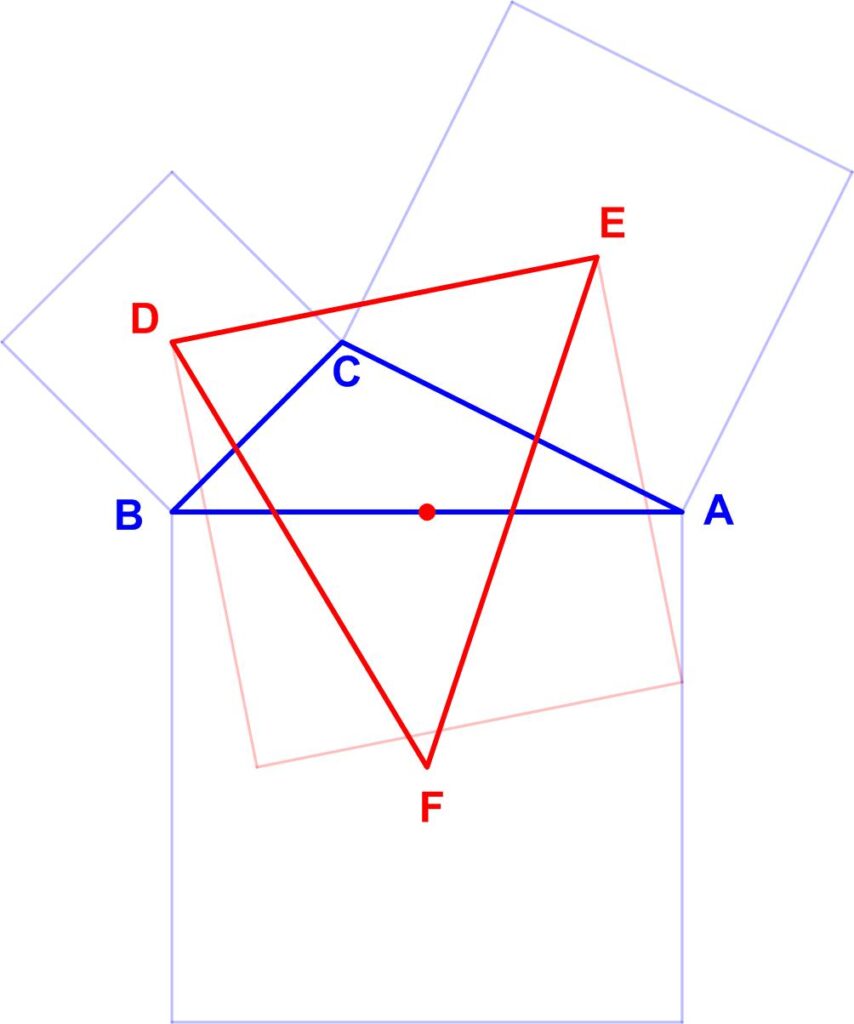
Professor Euclide Paracelso Bombasto Umbugio has once again retired to his tour d’ivoire where he is now delving into the supersophisticated intricacies of the works of Grassmann, as elucidated by Forder’s Calculus of Extension. His goal is to prove Neuberg’s Theorem:
If D, E, F are the centers of squares described externally on the sides of a triangle ABC, then the midpoints of these sides are the centers of squares described internally on the sides of triangle DEF. [The accompanying diagram shows only one internally described square.]
Help the dedicated professor emerge from his self-imposed confinement and enjoy the thrill of hyperventilation by showing how to solve his problem using only highschool, synthetic, Euclidean, ‘plain’ geometry.”
Alas, my plane geometry capability was inadequate to solve the puzzle that way, so I had to resort to the sledge hammer of analytic geometry, trigonometry, and complex variables.
See Neuberg’s Theorem
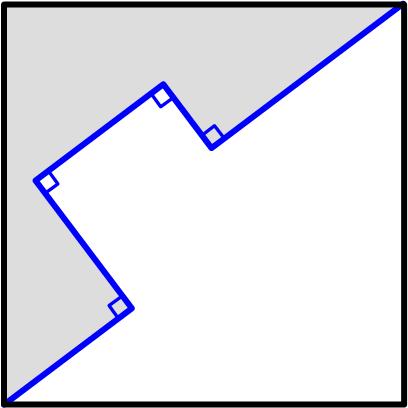 This is a nice problem from the UKMT Senior Mathematics Challenge for 2022:
This is a nice problem from the UKMT Senior Mathematics Challenge for 2022:
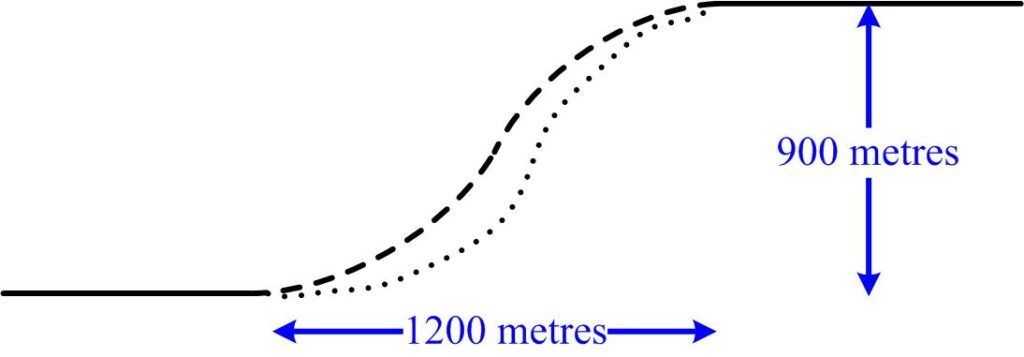 This is an interesting problem from the Scottish Mathematics Council (SMC) 2014 Senior Math Challenge .
This is an interesting problem from the Scottish Mathematics Council (SMC) 2014 Senior Math Challenge . This is another stimulating little problem from the 2022 Math Calendar.
This is another stimulating little problem from the 2022 Math Calendar. This math problem from Colin Hughes’s Maths Challenge website (mathschallenge.net) hearkens back to basic physics.
This math problem from Colin Hughes’s Maths Challenge website (mathschallenge.net) hearkens back to basic physics. This turned out to be a challenging puzzle from the 1980 Canadian Math Society’s magazine, Crux Mathematicorum.
This turned out to be a challenging puzzle from the 1980 Canadian Math Society’s magazine, Crux Mathematicorum.