 This is the second part of the problem from Raymond Smullyan in the “Brain Bogglers” section of the 1996 Discover magazine.
This is the second part of the problem from Raymond Smullyan in the “Brain Bogglers” section of the 1996 Discover magazine.
“On another occasion, Al made a mixture of water and wine. There was more water than wine—in fact, the excess of water over wine was equal to one-fourth the quantity of wine. Al then added 12 ounces of wine, at which point there was one ounce more of wine than water.
According to another version of the story, before Al added the 12 ounces of wine, he first boiled off 12 ounces of water (the net effect being that he replaced 12 ounces of water with wine), and again there was one more ounce of wine than water.
Would there be more mixture present at the end of the first version or the second?”
I found this statement a tad ambiguous with the result that I found two possible solutions: the one Smullyan gave and another, surprising one.

 This is a relatively simple problem from the inventive Raymond Smullyan in the “Brain Bogglers” section of the 1996 Discover magazine.
This is a relatively simple problem from the inventive Raymond Smullyan in the “Brain Bogglers” section of the 1996 Discover magazine.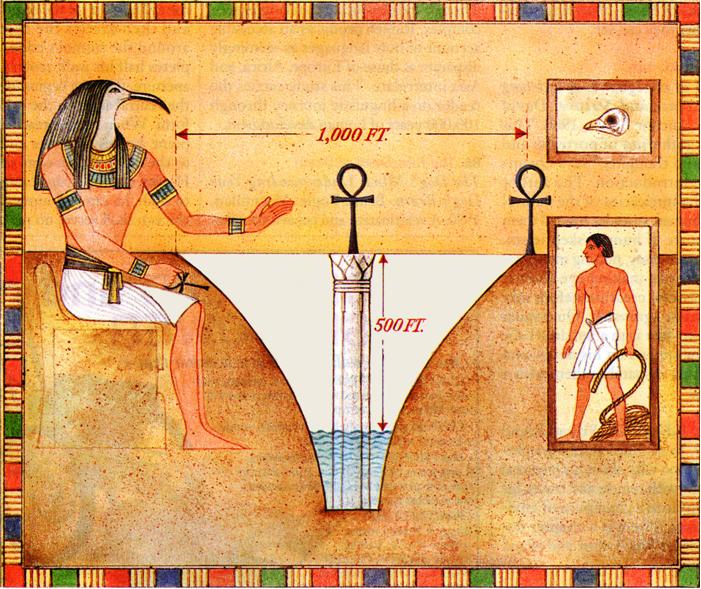 This is a nice puzzle from Clifford Pickover in the 1996 Discover magazine’s Brain Bogglers.
This is a nice puzzle from Clifford Pickover in the 1996 Discover magazine’s Brain Bogglers. Here is a collection of puzzles from the great logic puzzle master Raymond Smullyan in a “Brain Bogglers” column for the 1996 Discover magazine.
Here is a collection of puzzles from the great logic puzzle master Raymond Smullyan in a “Brain Bogglers” column for the 1996 Discover magazine.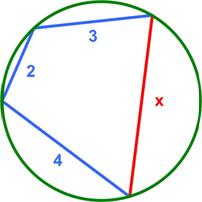
 This is a somewhat elegant problem from the 1987 Discover magazine’s Brain Bogglers by Michael Stueben:
This is a somewhat elegant problem from the 1987 Discover magazine’s Brain Bogglers by Michael Stueben: Here is another Brain Bogglers problem from 1987.
Here is another Brain Bogglers problem from 1987. This problem from the 1987 Discover magazine’s Brain Bogglers by Michael Stueben apparently traces back to 1770, though the exact reference is not given.
This problem from the 1987 Discover magazine’s Brain Bogglers by Michael Stueben apparently traces back to 1770, though the exact reference is not given.