 This is another challenging sum from the 2024 Math Calendar.
This is another challenging sum from the 2024 Math Calendar.
“Find x where x = et and
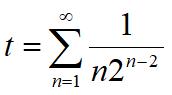 ”
”
As before, recall that all the answers are integer days of the month.
See Yet Another Sum for a solution.

 This is another challenging sum from the 2024 Math Calendar.
This is another challenging sum from the 2024 Math Calendar.
“Find x where x = et and
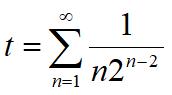 ”
”
As before, recall that all the answers are integer days of the month.
See Yet Another Sum for a solution.
 Continuing the logic thread, this is a nice logic problem from MathsJam Shout for April 2025.
Continuing the logic thread, this is a nice logic problem from MathsJam Shout for April 2025.
“The king of the spiders has four servants, and the servants have either 6, 7, or 8 legs. Servants with 7 legs always lie, and servants with 6 or 8 legs always tell the truth.
The king asks ‘How many legs do you four have in total?’, and the four spider servants (who are standing behind a table, so you can’t see their legs) answer 25, 26, 27, and 28, respectively.
Who is telling the truth?”
See The King of the Spiders for a solution.
 This is a logical puzzle from Muhammad Zain Sarwar on Puzzle Sphere.
This is a logical puzzle from Muhammad Zain Sarwar on Puzzle Sphere.
“Real Psychological Puzzle that will Test your Logical Thinking
Only 10% of Participants gave the Right Answer!
Imagine in front of you there are four cards placed on a desk. Each card has a number on one side and a color on the other. The visible faces of the cards show the following:
You are given a rule to verify:
“Every card that shows an even number on one side, then the opposite side must be red.”
Puzzle Statement
Your task is to determine which cards you must flip over to check whether this rule is being followed or not.
This question was part of a real psychological experiment.”
(I emphasized the “must” in the puzzle statement in order to limit the number of cards flipped to the minimum.)
See Logical Card Test for a solution.
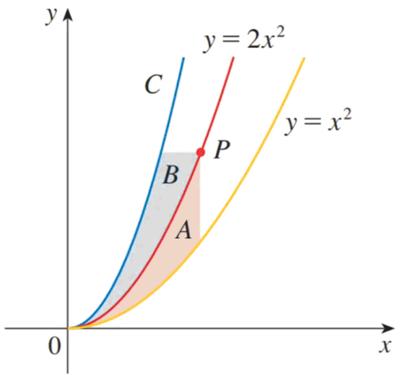 Here is another problem from BL’s Weekly Math Games.
Here is another problem from BL’s Weekly Math Games.
“For every point P on y = 2x2, areas A and B are equal. Find the equation for curve C.”
See Mystery Curve Puzzle for a solution
 Here is an entertaining puzzle from Futility Closet.
Here is an entertaining puzzle from Futility Closet.
“By Wikimedia user Efbrazil. Begin at the star. The number at your current position tells you the number of blocks that your next jump must span. All jumps must be orthogonal. So, for example, your first jump must take you to the 1 in the lower left corner or the 2 in the upper right. What sequence of jumps will return you to the star?”
See A Number Maze for solutions
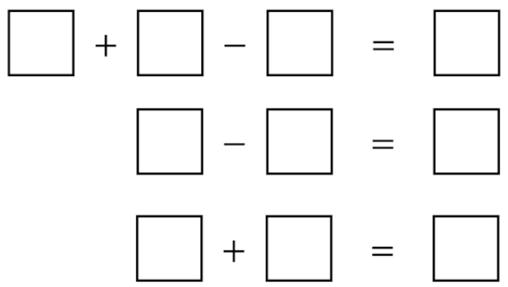 This is a somewhat unusual problem from Presh Talwalkar. It involves proving a student’s homework problem is impossible.
This is a somewhat unusual problem from Presh Talwalkar. It involves proving a student’s homework problem is impossible.
“I came across a homework problem described as “scary” on Reddit AskMath. You need to fill in the number sentences using the numbers 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 exactly once.
You should try a few possibilities to see why this is a challenging question. And do not waste too much time because the exercise is literally impossible! The challenge is, can you prove no solution exists?”
See Impossible Homework for a solution.
 On March 7 one of my favorite bloggers, Kevin Drum, passed away from a longtime fight with cancer. To say he will be sorely missed is great understatement. From my limited perspective, his was the last of the original type of weblog, namely one written by a single person with multiple postings per day. And his perspective was unique. It was the only blog I’ve seen that largely concentrates on data analysis of economics, science, medicine, societal trends, and on and on, in a clear, succinct, and informative manner. The text is further supported with simple graphs that provide visual clarity to the analysis.
On March 7 one of my favorite bloggers, Kevin Drum, passed away from a longtime fight with cancer. To say he will be sorely missed is great understatement. From my limited perspective, his was the last of the original type of weblog, namely one written by a single person with multiple postings per day. And his perspective was unique. It was the only blog I’ve seen that largely concentrates on data analysis of economics, science, medicine, societal trends, and on and on, in a clear, succinct, and informative manner. The text is further supported with simple graphs that provide visual clarity to the analysis.
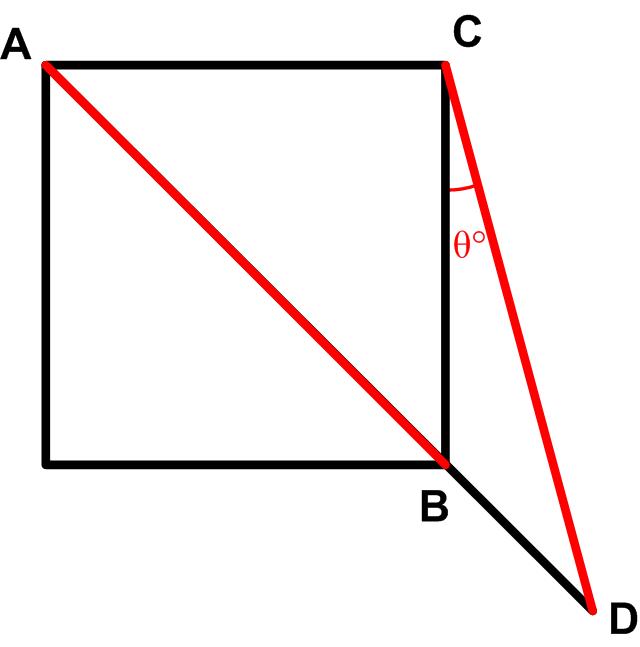 For me this turned out to be sort of a challenging problem from the 2025 Math Calendar.
For me this turned out to be sort of a challenging problem from the 2025 Math Calendar.
“Given equal line segments AB = CD, what is angle θ in degrees?”
See Elusive Angle for a solution
 This is a wicked variation of the ant problem on a stick by Peter Winkler.
This is a wicked variation of the ant problem on a stick by Peter Winkler.
“Twenty-four ants are randomly placed on a circular track of length 1 meter; each ant faces randomly clockwise or counterclockwise. At a signal, the ants begin marching at 1 cm/sec; when two ants collide they both reverse directions. What is the probability that after 100 seconds, every ant finds itself exactly where it began?”
See Circular Ant Problem for solutions.
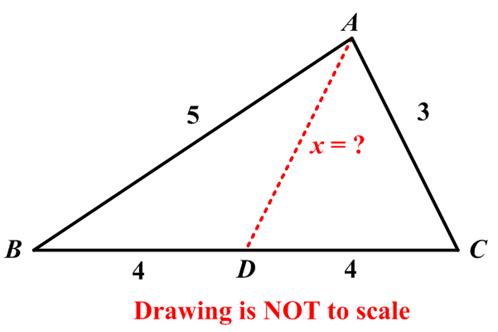 I think this turned out to be an even trickier problem than Alex Bellos thought.
I think this turned out to be an even trickier problem than Alex Bellos thought.
“Tricky triangle This one was sent in by a reader, aged 85, who first saw it in 1960. He is a roboticist who passed through Harvard, Princeton, Stanford and IBM. He says it is his favourite puzzle. ‘I’ve given this puzzle to perhaps 100 people. Over 80% have no idea how to solve it.’ What is the length of AD, the dashed line?”
See Tricky Triangle for solutions.