Tag Archives: soapbox

Cheshire Cat Paradigm

Leave a reply

I have been meaning to focus on this aspect of mathematics for some time.  It is a topic I elaborated in my “Angular Momentum” post. But I also think it has something to do with the difficulties that normal folks have with elementary math, in particular, numbers.  I thought I would dub it the Cheshire Cat Paradigm, involving the Cheshire Cat’s grin.

See the Cheshire Cat Paradigm.

(Update 6/7/2025) Contra Concrete Algebra

A recent posting has prompted me to address yet again my concerns about tying the learning of algebra so tightly to concrete objects and manipulations.

See Contra Concrete Algebra.

Logical Card Test

This is a logical puzzle from Muhammad Zain Sarwar on Puzzle Sphere.

“Real Psychological Puzzle that will Test your Logical Thinking

Only 10% of Participants gave the Right Answer!

Imagine in front of you there are four cards placed on a desk. Each card has a number on one side and a color on the other. The visible faces of the cards show the following:

  • 3
  • 8
  • Red
  • Brown

You are given a rule to verify:

“Every card that shows an even number on one side, then the opposite side must be red.”

Puzzle Statement

Your task is to determine which cards you must flip over to check whether this rule is being followed or not.

This question was part of a real psychological experiment.”

(I emphasized the “must” in the puzzle statement in order to limit the number of cards flipped to the minimum.)

See Logical Card Test for a solution.

Learning Mathematics

In one of our periodic FaceTime calls I found out that my granddaughter in 6th grade was interested in learning algebra and had gotten a book to help her out.  Clearly this initiative to get a head start prior to the normal course curriculum excited me, so I wrote what I thought was an insightful essay on the meaning and purpose of algebra.  Needless to say it was an abysmal failure.

That got me to thinking deeply about what it meant to learn mathematics and in particular symbolic algebra.

See Learning Mathematics

The Lure of Mathematics Conundrum

A prevalent theme of much of popular mathematical exposition and debates about mathematics education concerns how to interest a wider population in matters mathematical.  For the most part I feel that essays that try to present the “beauty” of mathematics are doomed to failure, as are most discussions of esthetics.  The underlying goal of such writing is a legitimate and laudable attempt to show the appeal of math.  But I fear it succeeds only with those already converted.  So is there another way?

See the Lure of Mathematics Conundrum

Angular Momentum

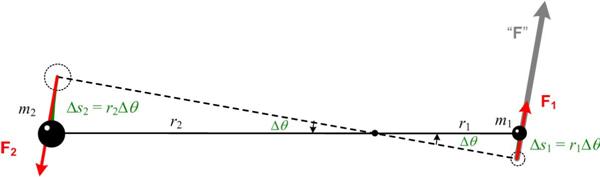I have always had a tenuous relationship with the concept of angular momentum, but recently my concerns resurfaced when I did my studies on Kepler, and in particular his “equal areas law” and Newton’s elegant geometric proof. I love the fact that a simple geometric argument, seemingly totally divorced from the physical situation, can provide an explanation for why the line from the Sun to a planet sweeps out equal areas in equal time as the planet orbits the Sun, solely under the influence of the gravitational force between them. However, modern physics books invariably cite the conservation of angular momentum as the “explanation.” I indicated before in my “Kepler’s Laws and Newton’s Laws” essay that this “explanation” irritated me. In this essay I go into detail about my reservations concerning this line of argument. See Angular Momentum.

Meditation on “Is” in Mathematics I – Zeno’s Paradox

This post is the first on a meditation on the nature of mathematics as I see it. I have been thinking about this for some time, and my thoughts were again stimulated by a March 2014 article I read in Slate by Brian Palmer that attempted a popularized explanation of the mathematical concepts associated with Zeno’s Paradox. It was a laudable effort that I applaud. So it is a bit churlish of me to critique it, but I felt its misconceptions got at the heart of some fundamental ideas about mathematics that I wanted to clarify.

The key idea exemplified in this article is the role “making it up” plays in math. That is, the general impression seems to be that math is dealing with things as they actually are if we can just be brought to see it. Whereas the idea that mathematicians make things up or define things is given little credence. For example, 0 x 2 “is” 0 doesn’t make any sense if you arrive at multiplication inductively from the intuitive idea of its being repeated addition. That is, 2 x 0 = 0 + 0 = 0 makes sense, but 0 x 2 = 0 does not. So mathematicians just say let’s define 0 x 2 = 0. If we do, it will be consistent with the other rules we have abstracted from the repeated addition idea, such as the commutative and distributive rules – that is, nothing breaks. (Try defining 0 x 2 to be any other number than 0 and see what breaks.) To put it another way, the reason we want to have 0 x 2 = 0 is for a different reason than we originally thought was meant by multiplication. We have extended the original idea into new territory. A similar thing happens with the advent of negative numbers. This is a very sophisticated idea and a challenge to present at an elementary stage.

In Part I, I will first present the article, heavily annotated with my critique. Then in Part II I will try to explain in more depth the admittedly philosophical concepts I am trying to get at.  See Meditation on “Is” in Mathematics I – Zeno’s Paradox.