Monthly Archives: August 2020

Family Values

Here is a collection of puzzles from the great logic puzzle master Raymond Smullyan in a “Brain Bogglers” column for the 1996 Discover magazine.

  1. ELDON WHITE HAS FOUR DOGS. One day he put out a bowl of dog biscuits. The eldest dog came first and ate half the biscuits plus one more. Then the next dog came and ate half of what he found plus one more. Then the next one came and ate half of what she found plus one more. Then the little one came and ate half of what she found and one more, and that finished the biscuits. How many biscuits were originally in the bowl?
  2. Eldon once bought a very remarkable plant, which, on the first day, increased its height by a half, on the second day by a third, on the third day by a quarter, and so on. How many days did it take to grow to 100 times its original height?
  3. In addition to four dogs, Eldon has four children. The youngest, Betty, is nine years old; then there are twin boys, Arthur and Robert; and finally there’s Laura, the eldest, whose age is equal to the combined ages of Betty and Arthur. Also, the combined ages of the twins are the same as the combined ages of the youngest and the eldest. How old is each child?
  4. “How about a riddle?” asked Robert. “Very well,” said Eldon. “What is it that is larger than the universe, the dead eat it, and if the living eat it, they die?”

Answer.

See Family Values  for solutions.

Another Cube Slice Problem

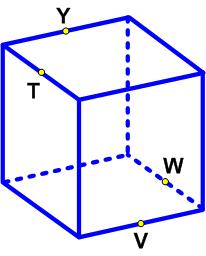This is a problem from the UKMT Senior Challenge for 2019.  (It has been slightly edited to reflect the colors I added to the diagram.)

“The edge-length of the solid cube shown is 2.  A single plane cut goes through the points Y, T, V and W which are midpoints of the edges of the cube, as shown.

What is the area of the cross-section?

A_√3_____B_3√3_____C_6_____D_6√3_____E_8”

Answer.

See Another Cube Slice Problem for solutions.

Serious Series

The following problem comes from a 1961 exam set collected by Ed Barbeau of the University of Toronto.  The discontinued exams (by 2003) were for 5th year Ontario high school students seeking entrance and scholarships for the second year at a university.

“If sn denotes the sum of the first n natural numbers, find the sum of the infinite series

.”

Unfortunately, the “Grade XIII” exam problem sets were not provided with answers, so I have no confirmation for my result.  There may be a cunning way to manipulate the series to get a solution, but I could not see it off-hand.  So I employed my tried and true power series approach to get my answer.  It turned out to be power series manipulations on steroids, so there must be a simpler solution that does not use calculus.  I assume the exams were timed exams, so I am not sure how a harried student could come up with a quick solution.  I would appreciate any insights into this.

Answer.

See Serious Series for a solution.

(Update 1/18/2021) Another Solution Continue reading →

Tree Trunk Puzzle

Here is another problem (slightly edited) from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos).

“Holmes and I were walking along a sleepy lane in Hookland, making our way back to the inn at which we had secured lodgings after scouting out the estates of the supposed major, C. L. Nolan. Up ahead, a team of horses were slowly pulling a chained tree trunk along the lane. Fortunately it had been trimmed of its branches, but it was still an imposing sight.

When we’d overtaken the thing, Holmes surprised me by turning sharply on his heel and walking back along the trunk. I stopped where I was to watch him. He continued at a steady pace until he’d passed the last of it, then reversed himself once more, and walked back to me.

‘Come along, old chap,’ he said as he walked past. Shaking my head, I duly followed.

‘It took me 140 paces to walk from the back of the tree to the front, and just twenty to walk from the front to the back,’ he declared.

‘Well of course,’ I said. ‘The tree was moving, after all.’

‘Precisely,’ he said. ‘My pace is one yard in length, so how long is that tree-trunk?’

Can you find the answer?”

Answer.

See the Tree Trunk Puzzle for solutions.