Monthly Archives: September 2019

Physical, Mathematical, and Personal Reality

The September 2019 Special Issue of Scientific American is a must read. Unfortunately it is behind a paywall, so you should purchase a copy at a store or digitally online. All the articles are fascinating and relevant, and address basic questions of epistemology—how do we know what we know? The first section, “Truth”, is the most pertinent to my thinking, as it covers three subjects I have been pondering for years.

Physical Reality. The first article in the section is “Virtually Reality: How close can physics bring us to a truly fundamental understanding of the world?” by George Musser. I have addressed this issue of physical reality in my article Angular Momentum, with an emphasis on the role of mathematics. Musser cites the difficulties of trying to understand quantum mechanics after almost one hundred years or the failure to marry quantum mechanics with Einstein’s theory of gravitation as possible indications that there might be limits to our human endeavor to comprehend physical reality. This frustration is not new:

Over the generations, physicists have oscillated between self-assurance and skepticism, periodically giving up on ever finding the deep structure of nature and downgrading physics to the search for scraps of useful knowledge. Pressed by his contemporaries to explain how gravity works, Isaac Newton responded: “I frame no hypotheses.”

Continue reading →

Circular Rendezvous Mystery

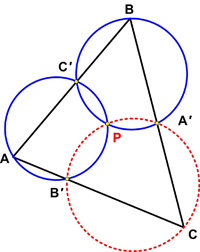Here is yet another surprising result from Colin Hughes at Maths Challenge.

“Problem
It can be shown that a unique circle passes through three given points. In triangle ABC three points A’, B’, and C’ lie on the edges opposite A, B, and C respectively. Given that the circle AB’C’ intersects circle BA’C’ inside the triangle at point P, prove that circle CA’B’ will be concurrent with P.”

I have to admit it took me a while to arrive at the final version of my proof. My original approach had some complicated expressions using various angles, and then I realized I had not used one of my assumptions. Once I did, all the complications faded away and the result became clear.

See Circular Rendezvous Mystery.

Flipping Parabolas

This is a stimulating problem from the UKMT Senior Math Challenge for 2017. The additional problem “for investigation” is particularly challenging. (I have edited the problem slightly for clarity.)

“The parabola with equation y = x² is reflected about the line with equation y = x + 2. Which of the following is the equation of the reflected parabola?

A_x = y² + 4y + 2_____B_x = y² + 4y – 2_____C_x = y² – 4y + 2
D_x = y² – 4y – 2_____E_x = y² + 2

For investigation: Find the coordinates of the point that is obtained when the point with coordinates (x, y) is reflected about the line with equation y = mx + b.”

Answer.

See Flipping Parabolas for a solution.

Fibonacci, Chickens, and Proportions

There is the famous chicken and the egg problem: If a chicken and a half can lay an egg and a half in a day and a half, how many eggs can three chickens lay in three days? Fibonacci 800 years ago in his book Liber Abaci (1202 AD) did not have exactly this problem (as far as I could find), but he posed its equivalent. And most likely the problem came even earlier from the Arabs. So we can essentially claim Fibonacci (or the Arabs) as the father of the chicken and egg problem. Here are three of Fibonacci’s actual problems:

“Five horses eat 6 sestari of barley in 9 days; it is sought by the same rule how many days will it take ten horses to eat 16 sestari.
A certain king sent indeed 30 men to plant trees in a certain plantation where they planted 1000 trees in 9 days, and it is sought how many days it will take for 36 men to plant 4400 trees.
Five men eat 4 modia of corn in one month, namely in 30 days. Whence another 7 men seek to know by the same rule how many modia will suffice for the same 30 days.”

By modern standards these problems all involve simple arithmetic to solve. But there are actually some subtleties in mapping the mathematical model to the situation, in which fractions, proportions, ratios, and “direct variation” get swirled into the mix—naturally causing some confusion.

Answers.

See Fibonacci, Chickens, and Proportions for a solution.

Trains – Pickleminster to Quickville

This is another train puzzle by H. E. Dudeney. This one has some hairy arithmetic.

“Two trains, A and B, leave Pickleminster for Quickville at the same time as two trains, C and D, leave Quickville for Pickleminster. A passes C 120 miles from Pickleminster and D 140 miles from Pickleminster. B passes C 126 miles from Quickville and D half way between Pickleminster and Quickville. Now, what is the distance from Pickleminster to Quickville? Every train runs uniformly at an ordinary rate.”