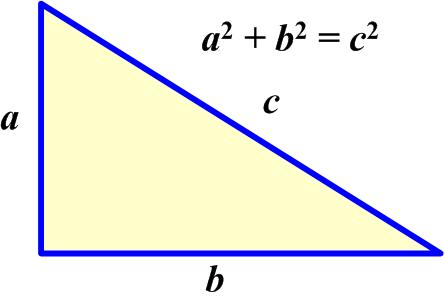
One of the joys of getting old is that you forget things. So one of the things I recall is that the converse of the Pythagorean Theorem is true, that is, if a triangle with short sides a and b and long side c is such that
a2 + b2 = c2,
then the triangle must be a right triangle with the angle between sides a and b being 90°. But I didn’t recall how to prove it. So I thought I would see if I could do it without looking up any sources.
See the Pythagorean Theorem Converse
This statement showed up recently at Futility Closet and I found it to be another one of those magical results that seemed so surprising. I don’t recall ever seeing this before.
“The radius of a circle inscribed in a 3-4-5 triangle is 1.
(In fact, the inradius of any Pythagorean triangle is an integer.)”
(A Pythagorean triangle is a right triangle whose sides form a Pythagorean triple.) Futility Closet left these remarkable statements unproven, so naturally I felt I had to provide a proof.
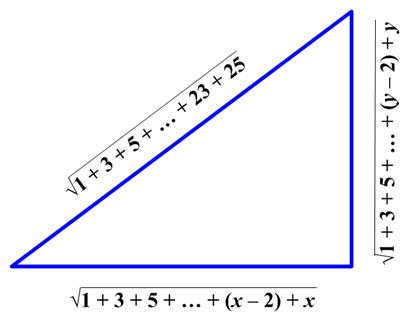This is an interesting problem from the United Kingdom Mathematics Trust (UKMT) Senior Math Challenge of 2008.
“The length of the hypotenuse of a particular right-angled triangle is given by √(1 + 3 + 5 + … + 23 + 25). The lengths of the other two sides are given by √(1 + 3 + 5 + … + (x – 2) + x) and √ (1 + 3 + 5 + … + (y – 2) + y) where x and y are positive integers. What is the value of x + y?”
See the Right Triangle with Roots for a solution.
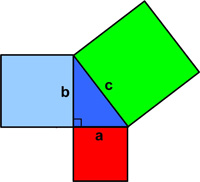All too frequently I come across the usual statements questioning why non-technical folks should bother studying math. A typical example is the Pythagorean Theorem. People say, “What good is that? I’ll never use it. So why bother?” Ah, the famous “utility” argument – as if everything worthwhile must be “useful.” I thought I would take this “useless” math example par excellence and show that, in fact, it harbors many of the best aspects of mathematics that anyone should find appealing. See the Pythagorean Theorem
