 I found this problem from the Math Challenges section of the 2002 Pi in the Sky Canadian math magazine for high school students to be truly astonishing.
I found this problem from the Math Challenges section of the 2002 Pi in the Sky Canadian math magazine for high school students to be truly astonishing.
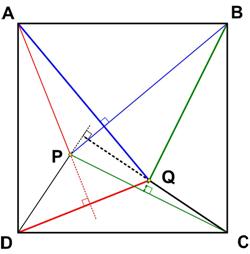
“Problem 4. Inside of the square ABCD, take any point P. Prove that the perpendiculars from A on BP, from B on CP, from C on DP, and from D on AP are concurrent (i.e. they meet at one point).”
How could such a complicated arrangement produce such an amazing result? I didn’t know where to begin to try to prove it. My wandering path to discovery produced one of my most satisfying “aha!” moments.
See the Mysterious Doppelgänger Problem
Update (12/27/2019) I goofed. I had plotted the original figure incorrectly. (No figure was given in the Pi in the Sky statement of the problem.) Fortunately, the original solution idea still worked.
 Here is another challenging problem from the 2004 Pi in the Sky Canadian magazine for high school students.
Here is another challenging problem from the 2004 Pi in the Sky Canadian magazine for high school students.
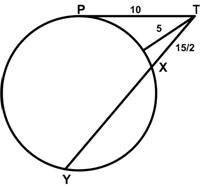 This is another problem from the Math Challenges section of the 2000 Pi in the Sky Canadian math magazine for high school students.
This is another problem from the Math Challenges section of the 2000 Pi in the Sky Canadian math magazine for high school students. I found this problem from the Math Challenges section of the 2002 Pi in the Sky Canadian math magazine for high school students to be truly astonishing.
I found this problem from the Math Challenges section of the 2002 Pi in the Sky Canadian math magazine for high school students to be truly astonishing.